Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2016-03-01 23:54:28
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Volume of irregular polyhedrons
(I) Let X denotes a polyhedron with vertices PQRSTUV where
the base PQRS is a square with sides 1/2 unit . TP and VQ are
straight lines each with length 1/8 unit and perpendicular to PQRS .
W is the mid-point of PQ while Y is the mid-point of RS . UW with
length 1/4 unit is perpendicular to PQRS also . Z is the mid-point of
TV .( also of UW )
Find the volume of X .
Offline
#2 2016-03-02 20:51:00
- Bob
- Administrator
- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons
hi mr.wong
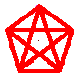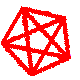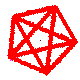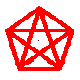
I cannot get a sensible polyhedron here. I've drawn the square PQRS and constructed the other points. P, T, U, V, Z, W and Q are all in a plane perpendicular to PQRS. Y lies in PQRS.
I've joined P to Q to R to S to T to U to V to P. That doesn't make a solid. And why tell me about Y as it doesn't feature in the problem? I think I'm missing something here. ![]()
As any polygon from some of these points will make a pyramid, I think I can get a volume when I know what the polyhedron is.
Please reply.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#3 2016-03-03 16:47:49
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi bob bundy , thanks for your reply !
You should not join V to P , instead you should join V to R , and
also S to T . If you like you may also join U to S and U to R .
Really the point Y is not necessary in the problem . I am sorry
for my statement has not been clear enough , is it better to denote
the polyhedron by PQRSTUVQP ?
Offline
#4 2016-03-03 20:44:44
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons
hi mr.wong
Thanks. That's helped a lot. I think this is the correct diagram. I haven't made it to scale. As well as the 'perspective view' on the left, I've also shown a side view looking along the line PQ.

I think you can treat this a two separate shapes: PQVTRS is a triangular prism with cross section QRV and length PQ; and a pyramid TVRSU with base TVRS and vertex U.
For the prism, work out the area of the cross section and multiply by the length.
For the pyramid, work out the area of the base and multiply by 1/3 of the perpendicular height. You need to do some calculations to get the measurements for this. In the rectangle TVRS calculate VR. The perpendicular height is the length of a line that is at right angles to ZY and measured from U. Take care to use the right distances here. On the side view the true length of U to 'RYS' will be UY so you will need the point Y after all ![]() . You can use trig. to get angles ZYW and UYW and hence calculate UYZ. From there you can calculate the distance UX where X is the 'foot' of the perpendicular from U to the line YZ extended, as you will know UY and angle UYZ.
. You can use trig. to get angles ZYW and UYW and hence calculate UYZ. From there you can calculate the distance UX where X is the 'foot' of the perpendicular from U to the line YZ extended, as you will know UY and angle UYZ.
Hope that's enough to get you through this.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#5 2016-03-05 20:30:33
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons
Were you hoping I'd check this?
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#6 2016-03-05 20:47:57
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi bob bundy ,
Thanks much to your analysis to the problem and the nice diagrams !
Let us consider the prism firstly . Since the area of Δ TPS = 1/2 *
1/2 * 1/8 sq.unit while the height = 1/2 unit , thus the volume
of the prism = 1/64 ( about 0.0156 ) cu.unit
Then for the pyramid , ST can be found to be √(17/64 ) unit ,
Thus the area of the base STVR = 1/2 * √(17/64 ) = (√17)/16 sq.unit .
But for the height , it is too bad for me to find its value with trigonometry for I have forgotten most of the trigonometry ! I have to find the volume of the pyramid by other means .
Let us cut the pyramid into 2 halves through Δ UYZ , we choose the
portion UYSTZ , also a pyramid , and denoted by H .
For H we shall cut it into 2 parts again through Δ USZ ,
part 1 , the pyramid YSUZ will be denoted by H1 , while
part 2 , the pyramid TSUZ , will be denoted by H2 .
For H1 , the point S will be considered as the new vertex with Δ UYZ as base . As SY being perpendicular to Δ UYZ ,
thus the height of H1 will be 1/4 unit .
Since the area of Δ YWU = 1/2 * 1/2 * 1/4 = 1/16 sq.unit
while the area of Δ YWZ = 1/32 sq.unit , thus the area of
Δ UYZ = 1/32 sq.unit also . ( In fact since YW ⊥ UW , the
area of Δ UYZ may be found directly to be 1/2 * 1/2 * 1/8 =
1/32 sq.unit .) Thus the volume of H1 = 1/3 * 1/4 * 1/32 =
1/384 cu. unit .
For H2 , the point U will be considered as the new vertex
with Δ STZ as base .
The height of H2 , UZ = 1/8 unit , while the area of Δ STZ =
1/2 * 1/4 * √(17/64 ) = (√17) / 64 sq. unit . Thus the volume of H2 = 1/3 * 1/8 * (√17) / 64 = (√17) / 1536 cu.unit .
So the volume of H = H1 + H2 = 1/384 + (√17) / 1536
= ( 4 + √17)/ 1536 cu.unit
Therefore the volume of the original pyramid = ( 4 + √17)/ 768 cu .unit
( about 0.01 cu.unit )
( Since the area of the original pyramid = (√17)/16 sq.unit . Thus the
height with U as vertex = 1/( 4√17) + ( 1/16 ) unit ( about 0.12 unit ) )
Lastly the volume of the original polyhedron will be found to be
1/64 + 0.01 = 0.016 + 0.01 = 0.026 cu.unit (approximately )
Offline
#7 2016-03-05 23:45:40
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons
That's what I get too! ![]()
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#8 2016-03-06 14:54:42
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Thanks bob bundy !
Here is another problem , wish you will help .
Problem (II)
Let H denotes a polyhedron PQRSTUVWXYZ where the base is a
rt. ∟. Δ PRT with PR = PT = 1/2 unit . Q, S and U are
mid-points of PR , RT and TP respectively .VP , XQ , WR ,YS and
ZU are all ⊥ to Δ PRT , with VP = WR = YS = ZU = 1/4 un. and
XQ = 1/2 un.
Find the volume of H .
Offline
#9 2016-03-06 20:21:27
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons
hi
When the question just gives a list of the vertices like this, it is not obvious which points are meant to join to which. Here is my guess at a diagram:

It looks to me like a prism PUSR/VZYW, a pyramid VZYW/X and a pyramid USYZ/T
P doesn't look like a right angle here because of the perspective.
So get the areas of the shaded regions and it should be straight forward from there.
Note. The line XT lies in the plane of the two triangles so I could have omitted it to simplify.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#10 2016-03-07 21:41:23
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi bob bundy ,
Your diagram is indeed what I want . Originally I expect you will
arrange the vertices in an anti-clockwise direction , and with the
pentagon PVXWR facing me . Now with your diagram I can look from
the back and obtain more integral impression of the polyhedron .
The whole polyhedron , as you said , can be divided into 3 portions :
(i) pyramid USYZ/T , will be denoted by H1 .
(ii) pyramid VZYW/X , will be denoted by H2 .
(iii) prism PUSR/VZYW , with cross - section being a trapezium , will be
denoted by H3 .
I shall calculate their volumes one by one .
Thanks again and I promise next time I will make the statement more
clearly .
Offline
#11 2016-03-08 15:20:50
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
(i) For H1 , area of the base = 1/4* 1/4 = 1/16 sq. unit while
height = 1/4 un , thus volume of H1 = 1/3* 1/4 * 1/16 = 1/192 cu.un
(ii) For H2 , area of the base = ( 1/4 + 1/2 )/2 * 1/4 = 3/32 sq.un while
height = 1/4 un , thus volume of H2 = 1/3 * 1/4 * 3/32 = 1/128 cu.un
(iii) For H3 , area of the base = 3/32 sq.un while height = 1/4 un ,
thus volume of H3 = 1/4 * 3/32 = 3/128 cu. un
To sum up , volume of H = 1/192 + 1/128 + 3/128 = 7/192 cu.un
(about 0.036)
Offline
#12 2016-03-08 20:46:12
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons
hi,
Yes I get that too.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#13 2016-03-09 14:42:46
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi bob bundy ,
Another problem is waiting ! Thanks in advance .
Problem (III)
Let H denotes a polyhedron PQRSTUP/VWXYZ where the base is a
rt. ∟. Δ PRT with PR = PT = 1/2 unit . Q, S and U are
mid-points of PR , RT and TP respectively .VQ, WR ,XS ,YT and
ZU are all ⊥ to Δ PRT , with VQ = WR = YT = ZU = 1/4 un.
and XS = 1/2 un. ; X and Z , Z and P , P and V , V and X are
joined . Notice that XP and ZV are co-planed . XZPV seems to be a
kite with XZ = XV and ZP = PV . ( While XZTY in Problem (II) should be
a parallelogram with unequal adjacent sides .)
Find the volume of H .
Offline
#14 2016-03-09 21:04:50
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons

US = ZM = PU = UZ = MX (by midpoints )
so PZ = ZX.
That kite is therefore a rhombus (special case of a kite).
The method is similar to the previous question.
How many more of these have you got hidden away?
Have you got geogebra yet? You can download it free and then make your own diagrams.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#15 2016-03-10 17:50:29
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi bob bundy ,
You are right , XVPZX is a rhombus , in addition ,
both XVZ and VPZ are equilateral Δs .
Let (i) H1 denotes the pyramid P/QUZV ;
(ii) H2 denotes the pyramid X/VZYW and
(iii) H3 denotes the prism QUTR/VZYW
For (i) , height = 1/2 *√1/8 (= √1/32 un.) ,
area of base = √1/8 * 1/4 sq . un .
Thus vol. of H1 = 1/3 * 1/2* √1/8 * √1/8 * 1/4
= 1/192 cu.un.
For (ii) , height = 1/4 un. , area of base = (√1/8 +√1/2)/2 * 1/2 *√1/8
= 3/32 sq.un.
Thus vol. of H2 = 1/3 * 1/4* 3 * √1/8 * 1/2*1/2 *√1/8
= 1/128 cu un .
For (iii) , height = 1/4 un , area of base = 3/32 sq un .
Thus vol. of H3 = 1/4 * 3/32 = 3/128 cu un
To sum up , volume of H = 1/192 + 1/128 + 3/128
= 7/192 cu.un (about 0.036) [ exactly the same as Problem (II) ]
Offline
#16 2016-03-12 15:45:27
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi bob bundy ,
Here is another problem . Before I have learnt the Geogebra , please help me once more !
Problem ( 3 T ) :
Let PQRSTUP / VWXYZKV denotes a polyhedron with
rt. ∟. Δ PRT as base where PR = PT = 1/2 unit Q, S and U are mid-points of PR , RT and TP respectively .VP , WQ , XR ,YS , ZT and KU are all ⊥ to Δ PRT , with VP = XR = ZT = 1/6 un. and WQ = YS = KU
= 7/24 un. WYK forms a triangle.
Find the volume of the polyhedron .
Offline
#17 2016-03-14 20:49:34
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Volume of irregular polyhedrons

I've added three more points, L, M and N on the same level as V, X and Z (see red dotted lines)
This looks to me like a triangular prism PRT/VXZ, another LMN/KWY, and three pyramids WKLM/V, KYNL/Z and WYNM/X.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#18 2016-03-15 14:49:50
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi bob bundy ,
Many thanks again !
Now let us cut the polyhedron into 2 layers along VMXNZLV ,
the lower part is a triangular prism with height 1/6 un and area 1/2* 1/2* 1/2
= 1/8 sq un . Thus its vol = 1/6 * 1/8 = 1/48 cu un .
We shall denote the upper part by H , which can further be dissected into 4 portions .
The 1st one being a pyramid , V/WKLM , will be denoted by H1 .
The 2nd one also a pyramid , Z/KYNL , will be denoted by H2 .
The 3rd one also a pyramid , X/ WYNM , will be denoted by H3 .
The 4th portion remained is a prism , LMN/KWY, will be denoted by H4 .
The height of H1 is found to be √1/32 = 1/2 * √1/8 un , while the base
is a rectangle with area 1/8 * √1/8 sq un , thus vol of H1 = 1/3 * 1/2 * √1/8 *1/8 * √1/8
= 1/6 * 1/8 * 1/8 = 1/384 cu un
The height of H2 is 1/4 un , while the base is also a rectangle with area 1/4 * 1/8 sq un ,
thus vol of H2 = 1/3 * 1/4 * 1/4 * 1/8 = 1/384 cu un
The height and area of H3 is the same as H2 , thus the vol of H3 = 1/384 cu un .
The height of H4 is 1/8 un , while the base being a triangle with area 1/2 * 1/4 * 1/4
= 1/ 32 sq un , thus the vol of H4 = 1/ 256 cu un .
Thus the total volume of the polyhedron = 1/48 + 1/384 + 1/384 + 1/384 + 1/256
= 1/48 + 1/128 + 1/256 = 16/768 + 6/768 + 3/768 = 25/ 768 cu un .
Divided by the area of the base of the polyhedron , we also get its average height
= (25/768)/ (1/8) = 25 / 96 un . ( about 0.26 ) while the square of 0.26 is about 0.0677 .
Offline
#19 2016-03-25 15:48:33
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Volume of polyhedron consisting of non-linear curves .
Related problem ( S1 ) :
Let T/ PQRS denotes a pyramid where PQRS is a square with
each side 1/2 unit . TP = 1/4 un. being perpendicular to the base .
Both TQ and TS are straight lines while TR is a quadratic curve
with equation z = 1/4 ( 1-2x) ( 1-2y) where PQ denotes the x-axis ,
PS denotes the y-axis and PT denotes the z-axis .
How to find the volume of the pyramid ?
( Perhaps we can cut the pyramid into 2 halves at TPR to get
2 pyramids S/ TPR and Q/TPR , but how to find the area of the
base TPR ? )
Offline
#20 2016-03-29 21:32:56
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
To find the area of the quasi-triangle TPR , let us at first re-arrange
the equation z = 1/4 ( 1-2x) ( 1-2y) to z = 1/4 (2x-1) (2y-1) .
Since PR is symmetric in x and y , thus z = 1/4 (2x-1) (2y-1) may
be simplified to z = 1/4 (2x-1) (2x-1) = 1/4 ( 2x-1) ^ 2 .
Let PR denotes the w-axis , we can see that w = √2 * x ,
i.e. x = w / √2 .
Thus z = 1/4 ( 2w/ √2 - 1) ^ 2 . i.e. z = 1/4 [(√2) w -1] ^2 .
The length of PR may be found to be √1/2 un . Thus
the area of the quasi-triangle TPR may be found by ∫z dw from
0 to √1/2 = 1/4 * 1/3 ( √2 w - 1)^ 3
= 1/12 * [ (√2 * √1/2 - 1) ^ 3 -( √2 * 0 - 1) ^ 3 ]
= 1/12 * [( 1-1) ^ 3 - (-1)^ 3 ]
= 1/12 * 1
= 1/12 sq. un.
Assume that the volume of pyramid S/ TPR may be calculated as 1/3 * 1/4 * 1/12 = 1/144 cu. un . Thus twice the volume = 1/72 cu.un .
being the volume of pyramid T/ PQRS .
Dividing by the base PQRS , we also get its average height
to be ( 1/72 ) / (1/4) = 1/18 un . ( about 0.056 )
Offline
#21 2016-06-27 17:18:56
- thickhead
- Member
- Registered: 2016-04-16
- Posts: 1,086
Re: Volume of irregular polyhedrons
Hi bob bundy ,
Thanks much to your analysis to the problem and the nice diagrams !
Let us consider the prism firstly . Since the area of Δ TPS = 1/2 *
1/2 * 1/8 sq.unit while the height = 1/2 unit , thus the volume
of the prism = 1/64 ( about 0.0156 ) cu.unit
Then for the pyramid , ST can be found to be √(17/64 ) unit ,
Thus the area of the base STVR = 1/2 * √(17/64 ) = (√17)/16 sq.unit .
But for the height , it is too bad for me to find its value with trigonometry for I have forgotten most of the trigonometry ! I have to find the volume of the pyramid by other means .
Let us cut the pyramid into 2 halves through Δ UYZ , we choose the
portion UYSTZ , also a pyramid , and denoted by H .
For H we shall cut it into 2 parts again through Δ USZ ,
part 1 , the pyramid YSUZ will be denoted by H1 , while
part 2 , the pyramid TSUZ , will be denoted by H2 .
For H1 , the point S will be considered as the new vertex with Δ UYZ as base . As SY being perpendicular to Δ UYZ ,
thus the height of H1 will be 1/4 unit .
Since the area of Δ YWU = 1/2 * 1/2 * 1/4 = 1/16 sq.unit
while the area of Δ YWZ = 1/32 sq.unit , thus the area of
Δ UYZ = 1/32 sq.unit also . ( In fact since YW ⊥ UW , the
area of Δ UYZ may be found directly to be 1/2 * 1/2 * 1/8 =
1/32 sq.unit .) Thus the volume of H1 = 1/3 * 1/4 * 1/32 =
1/384 cu. unit .
For H2 , the point U will be considered as the new vertex
with Δ STZ as base .
The height of H2 , UZ = 1/8 unit , while the area of Δ STZ =
1/2 * 1/4 * √(17/64 ) = (√17) / 64 sq. unit . Thus the volume of H2 = 1/3 * 1/8 * (√17) / 64 = (√17) / 1536 cu.unit .
So the volume of H = H1 + H2 = 1/384 + (√17) / 1536
= ( 4 + √17)/ 1536 cu.unit
Therefore the volume of the original pyramid = ( 4 + √17)/ 768 cu .unit
( about 0.01 cu.unit )
( Since the area of the original pyramid = (√17)/16 sq.unit . Thus the
height with U as vertex = 1/( 4√17) + ( 1/16 ) unit ( about 0.12 unit ) )
Lastly the volume of the original polyhedron will be found to be
1/64 + 0.01 = 0.016 + 0.01 = 0.026 cu.unit (approximately )
The volume of pyramid is 1/96 and that of polyhedron =5/192 to be exact.
{1}Vasudhaiva Kutumakam.{The whole Universe is a family.}
(2)Yatra naaryasthu poojyanthe Ramanthe tatra Devataha
{Gods rejoice at those places where ladies are respected.}
Offline
#22 2016-06-27 23:02:53
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Hi thickhead ,
Does this mean ( 4 + √17)/ 768 can be simplified to
1/96 ?
Offline
#23 2016-06-28 01:55:24
- thickhead
- Member
- Registered: 2016-04-16
- Posts: 1,086
Re: Volume of irregular polyhedrons
The volume of pyramid=
{1}Vasudhaiva Kutumakam.{The whole Universe is a family.}
(2)Yatra naaryasthu poojyanthe Ramanthe tatra Devataha
{Gods rejoice at those places where ladies are respected.}
Offline
#24 2016-06-28 04:32:35
- thickhead
- Member
- Registered: 2016-04-16
- Posts: 1,086
Re: Volume of irregular polyhedrons
Your solution seemed too long for a simple solution and I had not gone through it. But now I find you have taken the height of pyramid as UZ but you have to take perpendicular distance of U from the inclined plane i.e draw a perpendicular from U to ST and take its length.
{1}Vasudhaiva Kutumakam.{The whole Universe is a family.}
(2)Yatra naaryasthu poojyanthe Ramanthe tatra Devataha
{Gods rejoice at those places where ladies are respected.}
Offline
#25 2016-06-28 15:54:45
- mr.wong
- Member
- Registered: 2015-12-01
- Posts: 252
Re: Volume of irregular polyhedrons
Thanks thickhead,
Due to my weakness in trigonometry , I solve the
problem in that clumsy method instead of your concise
way with trigonometry thus error will easily occur !
Offline
Pages: 1