Math Is Fun Forum

denis_gylaev

Member

Registered: 2015-03-19

Posts: 66

tough pyramid problem

Hi

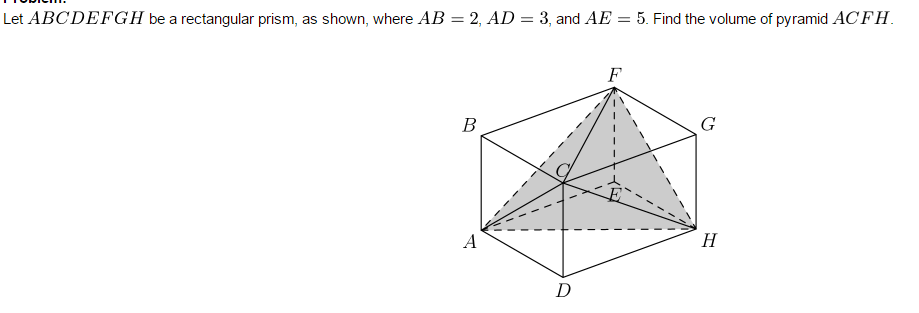
I am having a very hard time on this problem, and I can't seem to figure it out

https://gyazo.com/ff8dfae1227e4e7444c759d655b3f870

Here is the image-bobbym

thickhead

Member

Registered: 2016-04-16

Posts: 1,086

Re: tough pyramid problem

Hint: From the volume  of rectangular prism subtract the volumes of other remaining pyramids like ACFB whose volume can be found out easily.

If you want direct calculation it can be done by either vectors or 3 dimensional coordinate geometry.It depends at what level question is asked.

---

{1}Vasudhaiva Kutumakam.{The whole Universe is a family.}
(2)Yatra naaryasthu poojyanthe Ramanthe tatra Devataha
{Gods rejoice at those places where ladies are respected.}

thickhead

Member

Registered: 2016-04-16

Posts: 1,086

Re: tough pyramid problem

---

{1}Vasudhaiva Kutumakam.{The whole Universe is a family.}
(2)Yatra naaryasthu poojyanthe Ramanthe tatra Devataha
{Gods rejoice at those places where ladies are respected.}

thickhead

Member

Registered: 2016-04-16

Posts: 1,086

Re: tough pyramid problem

If it is difficult to find the area of one face of a pyramid, we can look into whether its projection is easy to find out. If so area decreases by a factor

  To compensate for this the height should be enhanced by a factor 

This is achieved by taking the height as a slant side making

with the height. this will be

to the projected area.Care must be exercised to see that the slant height is taken as the length from the vertex along the perpendicular to the projected area up to the point where it intersects the original base. In this case if we take the projection of area FAH on EFGH , we get triangle FEH whose area is 3 units.But there is some difficulty in finding slant height i.e length from C along CG until it meets the plane containing FA H. after concentrating for a while I felt if one would place another like prism flush with face EFGH  the farthest face being named E'F'G'H' , G'FH is identical with AFH and also in the continuation of the same plane. then the perpendicular from C, the vertex of the pyramid to the projection of the base viz. FEH would meet the original base at G'.  length CG'=2 CG=10. So the volume of the pyramid would be 1/3 *area FEH*CG'=1/3*3*10=10 units.
This concept was developed while dealing with the volume of a pyramid  in one of  the threads set by mr.wong

---

{1}Vasudhaiva Kutumakam.{The whole Universe is a family.}
(2)Yatra naaryasthu poojyanthe Ramanthe tatra Devataha
{Gods rejoice at those places where ladies are respected.}