Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2016-12-16 15:51:10
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
about Absolute Value....
Hi,
I study the absolute value maybe more than 2 times in my life,, when I was in the school and now and on the internet for myself
now I read (Absolute Value how far a number is from zero) .. then it is mean abs for 6 is 6 and -6 is 6
what is the meaning of that? and if it was about how far the number 6 from zero is the meaning of abs
then why -6 is 6 ? why the abs -6 is -6?
I apologize for such questions again and again.. I don't have another way to understand! sorry
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#2 2016-12-16 15:58:10
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: about Absolute Value....
Absolute Value is its distance from 0, for instance...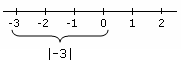 <--- We count the steps from 0( 1,2 and then 3.) We ignore the sign and count the net distance from -3 to 0(aka 3).
<--- We count the steps from 0( 1,2 and then 3.) We ignore the sign and count the net distance from -3 to 0(aka 3).
The absolute value of negative 6 is 6, since it is 6 away from 0 on the number line..
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#3 2016-12-16 15:58:22
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: about Absolute Value....
(Absolute Value how far a number is from zero)
Good Lord! Mathematicians and how they love to jargonize. Turning the simple, into the horribly complex. I have done several million calculations that have used the absolute value and never thought about it that way. Do I have a pea sized brain or are they incredibly deep or both? History will decide.
If you are using the absolute value to do a computation then all you have to remember is that the absolute value is always positive. Abs[5] = 5, Abs[-5] = 5. Always a positive value.
I see now that Mathegocart has provided a nice answer.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#4 2016-12-16 20:59:09
Re: about Absolute Value....
Last edited by zetafunc (2016-12-16 21:06:47)
Offline
#5 2016-12-16 22:50:06
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
#Mathegocart
yes thank you very much I got it now.
but can we say the abs -6 is -6 too? cause it is just a sign. what will happen if we say that
Last edited by Hannibal lecter (2016-12-16 23:01:40)
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#6 2016-12-16 22:53:46
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
thank you bobbym,
and #zetafunc sorry but I don't understand these symbols you provided, I'm not like you I just do simple mathematics I don't even know what is
and I wish to know what is these beautifull symbols
sorry
Last edited by Hannibal lecter (2016-12-16 23:19:01)
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#7 2016-12-16 23:18:35
Re: about Absolute Value....
Let me know if there's anything you want me to explain, I'm happy to help.
Offline
#8 2016-12-17 05:30:27
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: about Absolute Value....
#Mathegocart
yes thank you very much I got it now.
but can we say the abs -6 is -6 too? cause it is just a sign. what will happen if we say that
Previously said, the absolute value is the distance from 0. Distance, consequently, cannot be negative, and so the absolute value of -6 is simply 6.
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#9 2016-12-17 12:15:42
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Offline
#10 2016-12-17 13:32:09
- Monox D. I-Fly
- Member

- From: Indonesia
- Registered: 2015-12-02
- Posts: 2,000
Re: about Absolute Value....
Because u can either be a or -a.
Actually I never watch Star Wars and not interested in it anyway, but I choose a Yoda card as my avatar in honor of our great friend bobbym who has passed away.
May his adventurous soul rest in peace at heaven.
Offline
#11 2016-12-17 21:20:18
Re: about Absolute Value....
thank you very much Mathegocart
can I ask another question?
what is that mean :
http://store2.up-00.com/2016-12/1482020053631.png
what i u ?
and why +-a
Offline
#12 2016-12-19 08:36:50
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
thank you for this great example,
can I ask you another question it was difficult to me to solve it :-
<=or like this
<= 1please may I get the full solution for this? with its interval notation
Last edited by Hannibal lecter (2016-12-19 09:04:01)
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#13 2016-12-19 14:08:12
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: about Absolute Value....
This was initially irritating to solve( some paradoxes sprung forth ![]() ), though once you convert an absolute value into its alternative form, it becomes much more tolerable.
), though once you convert an absolute value into its alternative form, it becomes much more tolerable.
(convert to tolerable forme)
(square both sides)*
(isolate..)
(expand both convoluted functions)
(add a negative)
(divide, while noting the particular fact to switch signs.)
We are finished, with our bombardment of mathematical operations, we were able to find the solution out of this gargantuan inequality.
Last edited by Mathegocart (2016-12-19 14:08:30)
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#14 2016-12-20 05:55:33
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
Believe me if there is another way to help myself with, I'm sure I'll follow this way, but this is the only place that I can get help with a specific questions in math.
thank you very much.
so....is this the end of the solution? but how did you do that with an absolute value? ((( I mean we must take two possibilities once in >=0 and once in < 0 )))))???
please see this following picture, is the the solution of our lecturer in the university :- what is this? I really hop you to help me with full details about that
I always asking him about problems but our lecturer don't show respect to who ask him about that he learning us he just writing these problems without careful and caring ![]() ...
...
Last edited by Hannibal lecter (2016-12-20 06:03:06)
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#15 2016-12-20 06:45:42
Re: about Absolute Value....
Mathegocart's solution is fine, but as a point of caution, squaring an inequality (or an equation) can introduce solutions which don't satisfy the original inequality. If you do that, it's important in general to go back and check whether or not the solutions you've found are actually valid.
Offline
#16 2016-12-20 07:13:59
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
The important part to take away from your lecturer's solution is that is equivalent to
but mathegocart didn't do like the lecturer did, what does it changed? how the solution is
,and the sol of the teacher is :
, U {-1}.it's important in general to go back and check whether or not the solutions you've found are actually valid.
but how to do that? I mean how to check wether or not the solution is valid or not????
how did you know the solution was fine please help with that...
Last edited by Hannibal lecter (2016-12-20 07:20:32)
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#17 2016-12-20 07:21:12
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: about Absolute Value....
Believe me if there is another way to help myself with, I'm sure I'll follow this way, but this is the only place that I can get help with a specific questions in math.
thank you very much.so....is this the end of the solution? but how did you do that with an absolute value? ((( I mean we must take two possibilities once in >=0 and once in < 0 )))))???
please see this following picture, is the the solution of our lecturer in the university :- what is this? I really hop you to help me with full details about that
http://store2.up-00.com/2016-12/1482256157981.jpg
I always asking him about problems but our lecturer don't show respect to who ask him about that he learning us he just writing these problems without careful and caring
...
Sometimes it is more intuitive to explain it in the alternate form, which is also applicable for absolute values.
And yes, heed zetafunc's warning, sometimes it can introduce extraneous solutions.
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#18 2016-12-20 07:28:29
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
Sometimes it is more intuitive to explain it in the alternate form, which is also applicable for absolute values.
And yes, heed zetafunc's warning, sometimes it can introduce extraneous solutions.
may you please solve it like my lecturer did but in simple way without these strange number lines and +++ or ---
if you have a free time please, I need you sol with your elegant words and short steps. with greater and smaller and with interval notations.
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#19 2016-12-20 07:30:22
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: about Absolute Value....
Mathegocart wrote:Sometimes it is more intuitive to explain it in the alternate form, which is also applicable for absolute values.
And yes, heed zetafunc's warning, sometimes it can introduce extraneous solutions.may you please solve it like my lecturer did but in simple way without these strange number lines and +++ or ---
if you have a free time please, I need you sol with your elegant words and short steps. with greater and smaller and with interval notations.
Hmmm, those number lines are invaluable in visualizing the sets the inequalities include.
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#20 2016-12-20 07:32:11
Re: about Absolute Value....
(Since we know , then we don't need to worry about this possibility.Thus, if then
So now you know that the values for which your inequality hold are:
andThe intersection of these sets is . That is, the result of combining the above two inequalities is
To summarise, the left-hand side of what your lecturer wrote is fine. For the rest, see the above.
Last edited by zetafunc (2016-12-20 12:10:27)
Offline
#21 2016-12-20 07:37:36
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: about Absolute Value....
zetafunc wrote:The important part to take away from your lecturer's solution is that is equivalent tobut mathegocart didn't do like the lecturer did, what does it changed? how the solution is
,and the sol of the teacher is :
, U {-1}.zetafunc wrote:it's important in general to go back and check whether or not the solutions you've found are actually valid.
but how to do that? I mean how to check wether or not the solution is valid or not????
how did you know the solution was fine please help with that...
Put one value that supposedly satisfies the inequality(make sure it is convenient though), and see if you can verify it to be true. You could also graph it, but that is tedious.
Last edited by Mathegocart (2016-12-20 07:37:56)
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#22 2016-12-20 09:11:04
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
can't be a solution, because while
and what is that mean if I mean from where did you get |-1+3| there is just |x-3| and |x+1| in the expression I don't see |x+3|?
and do you mean it can't be equal to -1 because when we replace -1 by |x-3| ≤ |x+1| it will be |-1-3| ≤ |-1+1| then |-4| ≤ |0| and that is false it can't be -1, ... is that right? is I'm doing a good step or not....
So now you know that the values for which your inequality hold are:
and
The intersection of these sets is . That is, the result of combining the above two inequalities isTo summarise, the left-hand side of what your lecturer wrote is fine. For the rest, see the above.
you said inequality are hold x > -1
and x ≥ 1.
so where is number zero? why the inequality sol is not [0,∞) ?
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
#23 2016-12-20 11:49:51
Re: about Absolute Value....
do you mean it can't be equal to -1 because when we replace -1 by |x-3| ≤ |x+1| it will be |-1-3| ≤ |-1+1| then |-4| ≤ |0| and that is false it can't be -1, ... is that right? is I'm doing a good step or not....
Yes, that's what I meant.
you said inequality are hold x > -1
and x ≥ 1.so where is number zero? why the inequality sol is not [0,∞) ?
Which values of x satisfy both x > -1 and x ≥ 1?
Offline
#24 2016-12-23 09:30:19
- Hannibal lecter
- Member

- From: Iraq
- Registered: 2016-02-11
- Posts: 408
Re: about Absolute Value....
I think I got is thanks for your help
Wisdom is a tree which grows in the heart and fruits on the tongue
Offline
Pages: 1

