Math Is Fun Forum

!nval!d_us3rnam3

Member

Registered: 2017-03-18

Posts: 46

Tough question, need answer before tomorrow night. Thanks!

Let $\overline{PA}$ and $\overline{PC}$ be tangents from $P$ to a circle. Let $B$ and $D$ be points on the circle such that $B$, $D$, and $P$ are collinear. Prove that $AB \cdot CD = BC \cdot DA$.

I've already tried Power of a Point and similar triangles, but I can't seem to get anything to work. Can someone help me directly? By the way, don't post another link from this website, as I've probably checked that one already. Many thanks!

P.S. I need the answer before Saturday night.

---

"If we wanna be great, we can't just sit on our hands" - 2017 NFL Bears draft

Bob

Administrator

Registered: 2010-06-20

Posts: 10,621

Re: Tough question, need answer before tomorrow night. Thanks!

hi !nval!d_us3rnam3

Welcome to the forum.

Homework due again?

Backgound reading here:

http://www.mathisfunforum.com/viewtopic.php?id=22506

Hint:  Use the angle between a chord and a tangent is equal to the angle made by the chord to show angle BDC = angle BCP and hence that triangles PCB and PDC are similar.

Do a similar thing for triangles PDA and PAB.

Also note that PA = PC.

Writing ratios for PB/PA should enable you to complete this.

Bob

---

Children are not defined by school ...........The Fonz
You cannot teach a man anything;  you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you!  …………….Bob

!nval!d_us3rnam3

Member

Registered: 2017-03-18

Posts: 46

Re: Tough question, need answer before tomorrow night. Thanks!

I've already proved similar triangles. Just need a little help going from there. Can you help me through the ratios? Most of the time I get the same result as using Power of a Point.

I'll be on this forum fairly actively if I need any homework help.

---

"If we wanna be great, we can't just sit on our hands" - 2017 NFL Bears draft

Bob

Administrator

Registered: 2010-06-20

Posts: 10,621

Re: Tough question, need answer before tomorrow night. Thanks!

When I'm working with similar triangles I write equivalent points in the same order, to make it easier to generate ratios; thus:

PDA
PAB

So PB/PA involves taking the first and third letters from the bottom three and the first and third from the top three.  I've underlined the ones I mean.

So I can set that equal to another ratio taken in the same way.  As  I want DA and AB in the final answer, it makes sense to take them; so:

So that's half way there.

Now your turn.

Repeat for the other pair of similar triangles, again looking to make PB/PA.  Except there's no PA this time.  No worries;  because the two tangents are equal, so you can use PB/PC.

Bob

ps.  I've never heard of "power of a point".  Would you care to explain when you get time?

---

Children are not defined by school ...........The Fonz
You cannot teach a man anything;  you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you!  …………….Bob

!nval!d_us3rnam3

Member

Registered: 2017-03-18

Posts: 46

Re: Tough question, need answer before tomorrow night. Thanks!

Power of a point, in this diagram, looks like PA^2 = PD*PB = PC^2.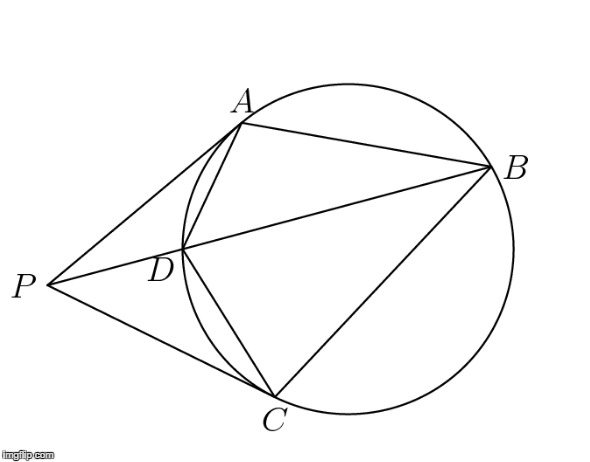

---

"If we wanna be great, we can't just sit on our hands" - 2017 NFL Bears draft

Bob

Administrator

Registered: 2010-06-20

Posts: 10,621

Re: Tough question, need answer before tomorrow night. Thanks!

My thanks,  !nval!d_us3rnam3

I've never heard it called that but, as you will see from this link, I did know this:

http://www.mathisfunforum.com/viewtopic … 92#p368592

Bob

---

Children are not defined by school ...........The Fonz
You cannot teach a man anything;  you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you!  …………….Bob