Position a rotated, variable sized rectangle

renevanderlende · 2020-04-20 01:06:44

Hi All,

I have a variable sized rectangle, a slanted ribbon, which I want to place in the top/right corner of a webpage.
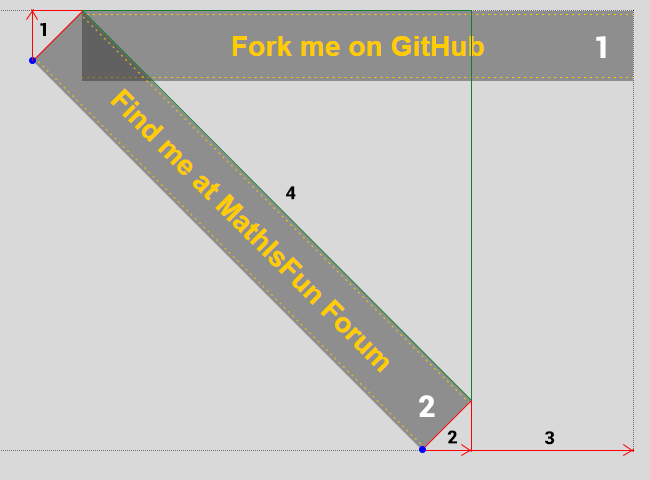
In the below images I can see what needs to be done (move ribbon distance 1 up and distance 2+3 to the right),
but I cannot find proper equation for distance 2+3.

Could you please help me and show the proper equation for going distance 2+3 right?

Variables:

y = mx + b for
height: points p1(320, 24) p2(1920, 32) => 0.5x + 22.4 => height = hm * x + hb
width: points p1(320,180) p2(1920,260) => 5x + 164 => width = wm * x + wb

rotation: 45 degrees
sqrt2: 1.4142 (to get side of a square from the hypotenuse, 4 significant decimals is more than enough)
scale: 2.5 (in the attached images)

In the below image you can see 2 rectangles (numbers in 'white'),
- one horizontal (1, 'Fork...', used for reference) and
- one slanted (2, 'Find...', which is actually a horizontal rectangle like (1), but rotated 45 degrees around its top/left corner)
- distances (in 'black')
- red and green rectangles to find hypotenuses
- the blue dots are the designated 'bottom/left' and 'bottom/right' corners of rectangle(2)
- the corners depicted by the blue dots need to be placed exactly on the dotted lines (top and right)

Equation for side of a rectangle: side = hypotenuse / sqrt2. Here the hypothenuse is equal to the height of rectangle(2):

- distances 1 (and 2) = (hm * x + hb) / sqrt2 * scale, which I tested and this proved to be correct
- distance 4 = (wm * x + wb) / sqrt2 * scale (not tested, but if the above is correct, then this is too)

- for now, the following equation to move the ribbon right seems to work
distance 2+3 = (wm * x + wb) / sqrt2 * scale * 0.545 (image 2), but does not yield the correct value and is actually cheating as I found 0.545 by trial and error...

Problem:

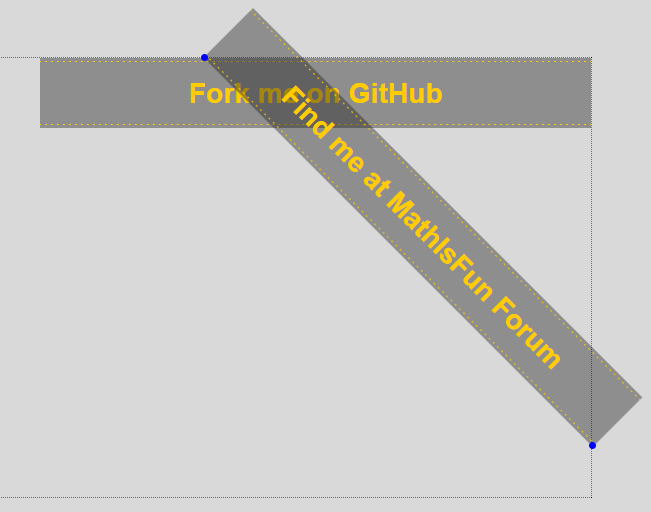
Final result (manually positioned!):

(You should see 2 images. If not go here examples)

Bob · 2020-04-20 23:20:34

hi renevanderlende

I'm sure I can sort this out but there are too many things you haven't explained yet.

y = mx + b for
height: points p1(320, 24) p2(1920, 32) => 0.5x + 22.4 => height = hm * x + hb
width: points p1(320,180) p2(1920,260) => 5x + 164 => width = wm * x + wb

What line is this? Where are those points on the diagram? What height? hm? hb? width? wm? wb?

I'm assuming you want the slanting ribbon to be at 45 degrees.

As for the two images: I'm assuming the top one is what you'd like and the bottom is what you've got. So there's some dodgy algebra somewhere. But without the above I'm confused. As you know that happens quiet often so please answer he above questions and then I'll have a look.

Stay safe,

Bob

renevanderlende · 2020-04-21 03:09:19

LOL,

I have a habbit of yabbering a lot and saying zilch, sorry for that. Quite some piece of text, though?

- Rectangle(1) is there for reference only, to show the initial location of rectangle(2) before it is rotated 45 degrees. You can safely ignore rectangle(1).
- I did not want to use too much CSS-like syntax and as you asked for values the last time I posted a problem, I tossed in a few I had calculated before.

However....

I think we have a programmer versus mathematician problem, we can read eachothers work, but don't fully speak the same language (I noticed that too during our previous conversation about scaling a text). After 40 years I am so used to thinking like a programmer it is hard not to, I'm sure you have something similar from a math perspective. Or...I am just a nincompoop (really wanted to use that word at least one time in my life!).

I constantly need to remind myself that you are probably not into CSS and therefore I have to translate 'code' to 'math' to explain my problem.

hm * x + hb depicts the height of a ribbon, hm and hb are just names of variables, not h*m and h*b (that's why programmers use names instead of letters only, and they do not automatically put/use a multiplification dot '.' between letters like mathematicians do).

wm * x + wb depicts the width of a ribbon, ditto

So....

x - always given (in CSS: 1vmin, where 'vmin' is a variable unit, which depicts a percentage of the smaller of the current browser viewport width and height. Extra: vw, vh and vmax units depict a percentage of the current browsers' width, height and maximum of the two respectively. So, in this case 1% of the minimumValueOf(viewportWidth,viewportHeight) ).

hm - height m value of the ribbon (in the given example: 0.5)
hb - height b value of the ribbon (= 22.4)
wm - width m value of the ribbon (= 5)
wb - width b value of the ribbon (= 164)

In pseudo CSS...

The below code moves rectangle(2) up and right as shown in image 2 (actual webpage result. Will NOT run properly in Internet Explorer 11. Firefox, Edge and Chrome are okay).

ribbon-values {
/*
Need to be filled in by some programmer as per requirement.

I created an open-source tool to get these values. Like the one in mathportal, but my version returns CSS code.
responsive sizing tool 1.1
Extended version (very WIP) with demos and explanation of the math. Yah, been quite busy this week...
Resize the browser and you will see all kinds of sizing and scaling going on. All linear equations doing that, learned from 'MathIsFun', so, full credit to you guys!!
*/

hm: 0.5;
hb: 22.4;
wm: 5;
wb: 164;
scale: 2.5;
sqrt2: 1.4142;
}

ribbon {
/* showing relevant variables only: */

height: calc((hm * 1vmin + hb) * scale);
width: calc((wm * 1vmin + wb) * scale);

rotate(45deg);

/* distance 1 */
top: calc((hm * 1vmin + hb) / sqrt2 * scale);

/* distance 2 + 3, equation I can't find */
right: ?????

/* currently used for distance 2 + 3, but not correct */
right: calc((wm * 1vmin + wb) / sqrt2 * scale * 0.545)
}

Important to know: opposed to math in CSS location (0,0) is located at top/left instead of bottom/left. But that is usually a matter multiplying the result with -1 (maybe ignore this for now).

As you can see from the actual webpage result I gave mathematically sizing, rotating, and shifting up rectangle(2) all work as expected. All I need now is to get the proper math for shifting it right as distance 2+3 ('right' in CSS) = '(wm * 1vmin + wb) / sqrt2 * scale * 0.545' is only a workaround for the lack thereof.

Maybe it has something to do with multiplying/dividing/converting degrees to radians after the 45deg rotation? I have no clue whatsoever.

Hopefully somewhat less dodgy, but please let me know if there's too much programming going on, in that case I will try my luck elsewhere, no biggy.

Rene

Last edited by renevanderlende (2020-04-21 03:16:19)

renevanderlende · 2020-04-21 14:17:41

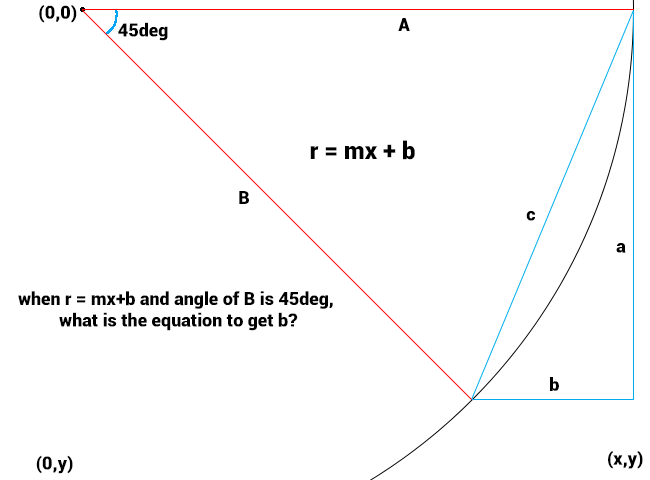
In addition to my previous post, I think I have been able to simplify my problem. Beware though, I am bad at math and while I may literally see a relation with my eyes, I really have no idea if I the below image is algebraicallilly correct.

I drew a circle (center at 0,0) with radius r = mx + b (the width of my ribbon) and a line B of length r (or mx + b) with an angle of 45 degrees. As you can see I (think I can) define a triangle a,b,c and obviously I see Pythagoras making an entrance. I just cannot connect the dots....

What is the algebraic equation for b when I only have (0,0), 45 degrees and y=mx+b to work with? (without using any values, that is)

Yes, I'm aware I should have picked up growing daisies...

Last edited by renevanderlende (2020-04-21 14:28:00)

Bob · 2020-04-21 22:33:35

hi Rene,

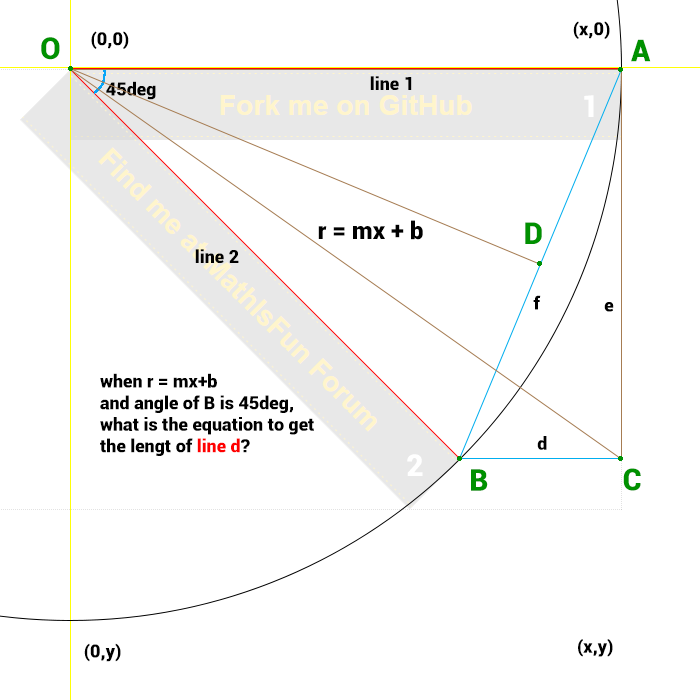
Now you're in my field of expertise. A geometric diagram. Almost perfect. Just one thing missing is to label the vertices so we know what lengths and angles are being used. Not to worry though. I can supply those now.

I'll call the origin O, the point on the right end, A and the point where the part circle ends, B. Finish with the point below A and to the right of B, I'll call C.

Triangle OAB is isosceles, that is to say it has to equal sides, OA and OB. So its bottom angles are equal too, OAB = OBA = 67.5 because the three angles must add up to 180.

As OAC is 90, that means that angle BAC is 90- 67.5 = 22.5 and angle ABC is 67.5 again, (trace out the Z shape from O to A to B to C, that's what geometers call alternate angles).

If you also draw a line from O to the midpoint of AB, say D, then triangle ODB is right angled so we can use trig.

BD = r.cos(67.5) so AB = 2r.cos(67.5)

BC = AB.cos(67.5) = 2r.cos(67.5) times cos(67.5)

67.5 in radians is 3pi/8

Bob

renevanderlende · 2020-04-22 03:21:26

Hi Bob,

Before anything else, please confirm that the below image depicts your previous explanation before I dive into the math and translate this to something my programmer head comprehends...

As I draw these things with Photoshop, the center of AB = D is a bit by approximation (meant as center, though).
I also adjusted the text a bit '...line d' and 'd' were previously '...line b' and 'b'. Just to prevent confusion with the 'b' in r = mx+b, so you know.

renevanderlende · 2020-04-22 13:54:33

Hi Bob,

Awaiting your reply I decided to translate your tut into CSS. And guess what? It worked the first time around!

I am relieved and happy (as a toddler with a new pacifier).
For me distance 3 = 2r.cos(67.5) * cos(67.5) is easy enough to understand, the mathematical logic will take time to sink in, though.

Remember, as I am using rectangles instead of lines, I need to go up distance 1 and go right distance 2 (which both are derived from the height of the rectangle) depicted in the first image I posted. Using your tut and filling in the up and right values, the final (simplified) code looks like this:

- negative because I need to go above the top and beyond the right border
- use a scale factor for the output size of the ribbon
- ribbon height = hm * x + hb
- ribbon width = OA = OB = r = wm * x + wb
- sqrt2 = sqrt(2) = 1.4142...
- cos = cos(67.5) = 0.38268343
- can only use +,-,*,/

top = calc((hm * x + hb) / sqrt2 * scale * -1)
right = calc((((hm * x + hb) / sqrt2) + (2 * (wm * x + wb) * cos * cos)) * scale * -1)

And I didn't even need to use radians...

Now I need to take it up a notch and only work with 45deg, p1(x1,y1) p2(x2,y2) and put the full 'point slope' form into the eqation for both width and height of the rectangle, as well as the equation for cosine. It won't probably even compute (in CSS).

To humour you, the pure CSS (with 'custom variables'), just the parenthesis alone keep me awake at night:

.ribbon {
top : calc(((var(--hm) * var(--x) + var(--hb)) * var(--scale)) / var(--sqrt-2) * -1);
right: calc((((var(--hm) * var(--x) + var(--hb)) / var(--sqrt-2)) + (2 * (var(--wm) * var(--x) + var(--wb)) * var(--cos67dot5) * var(--cos67dot5))) * var(--scale) * -1);
}

Well, as long as it works.

Truly happy about this,
Thanks Bob!!

Last edited by renevanderlende (2020-04-22 13:57:31)

Bob · 2020-04-22 22:55:07

I'm glad we're making progress. If you want me to tackle the geometry where you have coordinates then you know now what to do. Supply a labelled diagram with the coords shown and say what measurements are needed.

Bob

renevanderlende · 2020-04-23 02:13:31

Thanks Bob, I will do that (as soon as I'm finished gloating and padding myself on the back).

But I think I will post a mini tutorial in the 'Coder's Corner', something like 'Why use algebra and trigonometry in CSS' referencing the above. This way I can safely link math to programming (less appropriate here in 'Help me!').

For now

BC = AB.cos(67.5) = 2r.cos(67.5) times cos(67.5)

is what I needed to get a good nights' sleep again!

Final Result, works in all (Windows) browsers (even IE11).

Final code (for IE11 to work properly, ribbon scale = 1.1):
top : calc(((0.5vmin + 1.4rem) * 1.1) / 1.4142 * -1);
right: calc((((0.5vmin + 1.4rem) / 1.4142) + (2 * (5vmin + 10.25rem) * 0.38268343 * 0.38268343)) * 1.1 * -1);

In the mean time I'm considering this topic done and dealt with...

Rene

Last edited by renevanderlende (2020-04-23 02:21:08)

renevanderlende · 2020-04-27 01:08:48

Gloating?? I meant glowing, arghh, NL-EN translations....

Bob · 2020-04-27 20:52:17

When I was at school, several centuries ago, we were made to analyse poetry. Why did the poet use this word? What does it add to the meaning of the piece? What 'ordinary' word does it replace?

So your post took me back, and I tried to analyse it that fashion. Oh, happy days, when we used to sit next to each other and go to the park. For your information the next phrase is " patting myself on the back " but don't worry. I realise that English is no longer under the control of the English and all that time we spent learning correct usage has ' gone out the window '. Your English is excellent and 100% better than my Dutch, which is probably limited to the words you've been kind enough to let us incorporate into our speech as though we thought of them. That's one thing that the English are so good at. And it leads to some laughable quotes like:

George Bush wrote:

"The problem with the French is that they don't have a word for entrepreneur."

Keep laughing and stay safe,

Bob

Math Is Fun Forum

#1 2020-04-20 01:06:44

Position a rotated, variable sized rectangle

#2 2020-04-20 23:20:34

Re: Position a rotated, variable sized rectangle

#3 2020-04-21 03:09:19

Re: Position a rotated, variable sized rectangle

#4 2020-04-21 14:17:41

Re: Position a rotated, variable sized rectangle

#5 2020-04-21 22:33:35

Re: Position a rotated, variable sized rectangle

#6 2020-04-22 03:21:26

Re: Position a rotated, variable sized rectangle

#7 2020-04-22 13:54:33

Re: Position a rotated, variable sized rectangle

#8 2020-04-22 22:55:07

Re: Position a rotated, variable sized rectangle

#9 2020-04-23 02:13:31

Re: Position a rotated, variable sized rectangle

#10 2020-04-27 01:08:48

Re: Position a rotated, variable sized rectangle

#11 2020-04-27 20:52:17

Re: Position a rotated, variable sized rectangle

Board footer