Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2021-03-28 10:21:11
- mathland
- Member
- Registered: 2021-03-25
- Posts: 444
Find Limit Given x(theta) & y(theta)...1
Given x(theta) = [10 cos(theta)]t and y(theta) = -16t^2 + [10 sin(theta)],
find the following:
lim x(theta)
theta--> pi/4 from the right
lim y(theta)
theta--> pi/4 from the right
Last edited by mathland (2021-03-28 10:23:03)
Offline
#2 2021-03-28 16:17:31
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: Find Limit Given x(theta) & y(theta)...1
Hello mathland.
Firstly, I'm presuming that the "t" also represents theta.

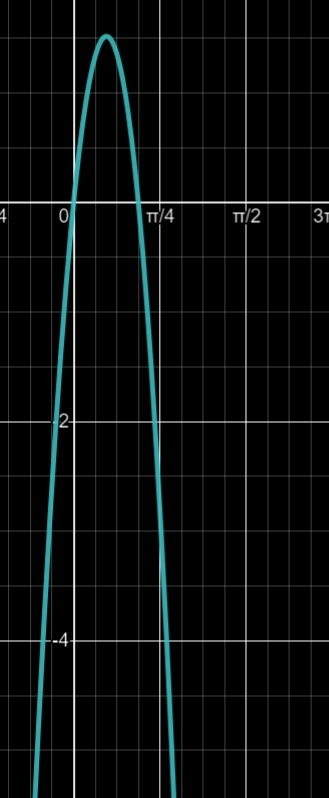
(A graph of x(theta). x is the vertical axis in this case and theta the horizontal.)
It is evident that if we stay to the right and move left, the function is moving towards the value 10cos(pi/4)(pi/4). This is approximately equal to 5.553.
As for your second question with lim y(theta), we see that the function approaches -16(pi/4) + 10 sin(pi/4). This value, to the thousandths, is -2.799.
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#3 2021-03-29 16:20:04
- mathland
- Member
- Registered: 2021-03-25
- Posts: 444
Re: Find Limit Given x(theta) & y(theta)...1
Hello mathland.
Firstly, I'm presuming that the "t" also represents theta.
https://i.postimg.cc/637pd2cy/Desmos-Graphing-Calculator.png
(A graph of x(theta). x is the vertical axis in this case and theta the horizontal.)It is evident that if we stay to the right and move left, the function is moving towards the value 10cos(pi/4)(pi/4). This is approximately equal to 5.553.
As for your second question with lim y(theta), we see that the function approaches -16(pi/4) + 10 sin(pi/4). This value, to the thousandths, is -2.799.
https://i.postimg.cc/FRbnCGDq/Desmos-Graphing-Calculator-2.png
Very good. Thanks.
Offline
Pages: 1