Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2021-04-03 10:46:55
- mathland
- Member
- Registered: 2021-03-25
- Posts: 444
Limit of Rational Function...1
Find the limit of (2x + 1)/(x + 4) as x tends to - 4 from the right side.
I know there's a vertical asymptote at x = -4. I think the best way to solve this problem is by graphing the function. I am not too sure about how to solve this problem algebraically.
I am thinking about the number line.
<---------------(-4)----------------->
What if I select values to the left and right of -4 but not including -4? By doing this, I will then know if the interval (-00, -4) is positive or negative and if the interval (-4, 00) is positive or negative.
Is this correct so far?
Offline
#2 2021-04-03 17:31:55
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: Limit of Rational Function...1
Heyya Mathland,
I'm noticing a trend with your threads - you're splitting each individual problem(which has the same underlying theme) into its each own thread. Generally it is preferred here to keep problems with the same underlying topic in the same thread to reduce clutter.
With regards to a potential algebraic approach, we can either consider factoring the numerator and demoniator and cancelling out like terms, splitting the fraction, using L'Hopital's laws, or using the properties of the limit.
Try using the product rule. The limit of a product is the product of the limits. Do you have it?
But yes, your current approach does work. It is a little rudimentary though.
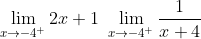
Do you know what to do from here?
EDIT 1:
> What if I select values to the left and right of -4 but not including -4? By doing this, I will then know if the interval (-00, -4) is positive or negative and if the interval (-4, 00) is positive or negative.
You're approaching from the right, so you don't need values to the "left" of four. Also, what is (-00, -4)? No such thing as negative 0 and why the two 00s? One 0 is fine. Besides, 0 is greater than -4, so it should appear as follows: (-4,0).
Last edited by Mathegocart (2021-04-03 17:41:55)
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#3 2021-04-03 23:30:38
- mathland
- Member
- Registered: 2021-03-25
- Posts: 444
Re: Limit of Rational Function...1
Heyya Mathland,
I'm noticing a trend with your threads - you're splitting each individual problem(which has the same underlying theme) into its each own thread. Generally it is preferred here to keep problems with the same underlying topic in the same thread to reduce clutter.With regards to a potential algebraic approach, we can either consider factoring the numerator and demoniator and cancelling out like terms, splitting the fraction, using L'Hopital's laws, or using the properties of the limit.
Try using the product rule. The limit of a product is the product of the limits. Do you have it?
But yes, your current approach does work. It is a little rudimentary though.
https://i.postimg.cc/kgNyn5vB/latex.gif
Do you know what to do from here?
EDIT 1:
> What if I select values to the left and right of -4 but not including -4? By doing this, I will then know if the interval (-00, -4) is positive or negative and if the interval (-4, 00) is positive or negative.
You're approaching from the right, so you don't need values to the "left" of four. Also, what is (-00, -4)? No such thing as negative 0 and why the two 00s? One 0 is fine. Besides, 0 is greater than -4, so it should appear as follows: (-4,0).
1. Thank you for letting me know not to split my threads. In other forums, posting more than one similar question per thread is not allowed. I thought the same applies here but now I see that it does not.
2. L'Hôpital's Rule involves taking the derivative of the numerator and denominator. I start Chapter 2 today or tomorrow. Learning a course one chapter at a time is the best way to assure the information is fully grasped. You see, I am learning Calculus 1 on my own. It is a course that I always wanted to take back in my college days but was afraid to, if that makes any sense to you.
3. Yes, I am familiar with the product rule for limits. It just didn't dawn on me to split the rational function into two separate functions, which is a great idea. I thank you for reminding me that this is legal in mathematics.
4. My friend, I don't know LaTex. So, in place of negative infinity I often use -00 and instead of positive infinity I often use 00.
5. You said:
"What if I select values to the left and right of -4 but not including -4? By doing this, I will then know if the interval (-00, -4) is positive or negative and if the interval (-4, 00) is positive or negative."
Yes, dividing the number line into several intervals is another approach. It reveals if the interval is positive or negative for a chosen value. I like what you said above about separating rational functions into separate functions and applying the product rule for limits. This is probably the best method in addition to graphing.
6. To answer your question, yes, I can take it from here.
Note: I also like posting several similar questions to provide others with practice problems to play with. I am sure there are college students here that appreciate several problems that they might be learning in class.
Offline
Pages: 1