Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2022-10-18 10:29:29
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Circle on circle
This is about intersecting a circle with another of different size
in on point in which both circles have the same slope.
Starting with the equation of a circle x²+y²=r² <=> y=sqrt(r²-x²).
Adding variables for shifting
(a for the x direction and b for the y direction):
(x−a)²+(y−b)²=r²
Solving it for y:
y = +/- sqrt(-a²+2*a*x+r²-x²)+b
The first derivative:
d/dx(sqrt(-a²+2*a*x+r²-x²)+b)=(a-x)/sqrt(-a²+2*a*x+r²-x²)
For the second circle: c=a2, d=b2, q=r2.
For the intersection point, this gives us the following equation system;
sqrt(-a²+2*a*x+r²-x²)+b=sqrt(-c²+2*c*x+q²-x²)+d
(a-x)/sqrt(-a²+2*a*x+r²-x²)=(c-x)/sqrt(-c²+2*c*x+q²-x²)
If we define the position of the second circle,
and their sizes, and only shift horizontally,
we still have a and x variable.
Am I on the right track,
and if so, Is there something wrong,
since we only have 2 equations here ?
Edit:
The centers of the circles and the intersection
are on the same line when the slopes match.
Maybe something could be done with that.
Last edited by mathdrop (2022-10-18 12:14:37)
Offline
#2 2022-10-18 22:35:21
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,810
Re: Circle on circle
hi mathdrop,
Is this the sort of thing you're after:

There are these equations:
...(1)...(2)
...(3)
Note x ad y are either points on one circle, or the other, or the straight line. There is one point on all three.
I haven't gone any further but it looks like all the square terms can be eliminated so that'll avoid square roots.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#3 2022-10-27 09:10:03
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on circle
There are 4 cases
in which the circles have one point
(same slope, there) in common.
Your graph depicts the first one.
If you move the little circle along the line,
you get the other cases.
I particularly thought of the third one,
but it should not make much difference,
mathematically.
Please describe in more detail,
what you are doing after the two circle equations.
Offline
#4 2022-10-27 21:22:38
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,810
Re: Circle on circle
As with the hyperbola question, the equations get really complicated without numbers.
I have labelled three of my equations (1) (2) and (3).
(1) + (2) - (3) gives
And the centre line is
As long as those are the correct equations for the circles and the centreline it shouldn't matter if the diagram is only one case out of several. The algebra will 'take care of that'.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#5 2022-10-30 01:01:54
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on circle
Please tell me, how you get to equation number 3
and the unlabelled one just before.
Offline
#6 2022-10-31 00:07:14
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,810
Re: Circle on circle
...(3)
This is Pythagoras. c-a is the horizontal distance between the centres and d-b is the vertical distance.
r+s is the distance between the centres.
(4) ... If the circles touch at (x,y) and a single line joins the centres and this point, then just get two expressions for its gradient and equate them.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#7 2022-11-02 08:45:03
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on circle
Regrading abcd one is unknown and the others are known,
so I move one circle either along x or y.
Can't believe I haven't seen the Pythagoras and maybe the other one.
However, I do not see how I might utilize this here yet,
and I still do not know why you do (1) - (2) + (3).
This is an intersection approach without considering the line
and any slopes:
(x-a)²+(y-b)²=r² <=> (x-a)²+(y-b)²-r²=0
(x-c)²+(y-d)²=s² <=> (x-c)²+(y-d)²-s²=0
Intersecting the circles:
(x-a)²+(y-b)²-r²=(x-c)²+(y-d)²-s² <=> f(x)=y=(a^2-2*a*x+b^2-c^2+2*c*x-d^2-r^2+s^2)/(2*b-2*d)
Somehow there should now be this cases:
0 solutions, 1 solution, 2 solutions.
But it says, that all reals are solutions.
Any clue ?
Offline
#8 2022-11-02 21:23:30
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,810
Re: Circle on circle
hi
I've realised that, although I've kept up this dialogue, I don't actually know what the question is. Help me out here:
What is given and what must be determined?
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#9 2022-11-03 08:42:50
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on circle
With the vertical movement, I mentioned In my last post,
I started to go more general as in the perspective, I started out with,
so horizontal movements should be enough.
I also move the small circle horizontally, and not perhaps along the blue line in your plot
(I missed to mention this while answering to your graph).
To imagine it, you could put the center of the small circle one square above the center of the big circle
and move the small circle horizontally (I imagine to the right) until it touches the big circle.
Known is b, c, d and the two radiuses of the circles.
Unknown is a (I probably should have omitted calling x an unknown in the threadstarter).
Edit: a must also be determined.
Last edited by mathdrop (2022-11-03 08:54:13)
Offline
#10 2023-02-20 03:52:17
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on circle
There is a geometric solution.
This one is by moving the big circle down the y-axis, till they touch.
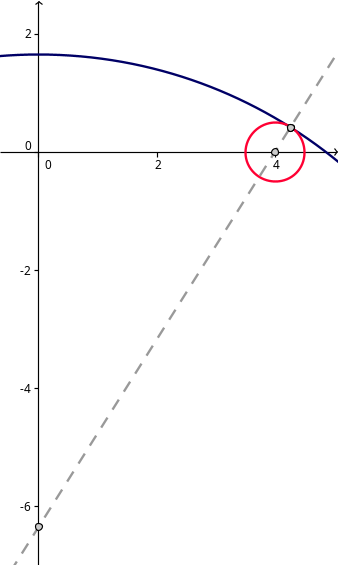
I'm still not entirely sure if I can not use calculus,
having 2 shifted circles, one with a free variable,
and finding the shift so they have one point in common, and why.
Maybe I should have taken derivatives in post 7 like so:
y=b +/- sqrt(-a^2+2*a*x+r^2-x^2)
y'=(+/- a -/+ x)/sqrt(-a^2+2*a*x+r^2-x^2)
y=d +/- sqrt(-c^2+2*c*x+s^2-x^2)
y'=(+/- c -/+ x)/sqrt(-c^2+2*c*x+s^2-x^2)
(a-x)/sqrt(-a^2+2*a*x+r^2-x^2)-y=(c-x)/sqrt(-c^2+2*c*x+s^2-x^2)-y
<=>
(a-x)/sqrt(-(a-r-x)*(a+r-x))+(x-c)/sqrt(-(c-s-x)*(c+s-x))=0
a=+/- (c*r-r*x+s*x)/s
c=+/- (a*s+r*x-s*x)/r
This seems to be solved now.
Just with the derivatives (slopes) I can just use horizontal shifting,
because they do not contain values for vertical shifting.
If needed, I probably could work around or use another approach, here.
In the geometric example I could have as well moved the little circle to the right.
Last edited by mathdrop (2023-02-20 10:46:37)
Offline
Pages: 1