Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2007-02-20 18:12:03
- fredekr
- Member
- Registered: 2007-02-20
- Posts: 5
Marquis De L'Hopital optimization problem
Can anybody outline a symbolic solution for the Marquis De L'Hopital optimization problem on this site?
It's at:
http://www.mathsisfun.com/marquis.html
I can solve it numerically in two different ways, but my analysis gives me a nasty relation that I didn't want to try to differentiate symbolically since it didn't look like it would be solvable.
best,
Kevin
Offline
#2 2007-02-23 15:17:21
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Marquis De L'Hopital optimization problem
If you graph delta hypotenuse over delta y, and then find where the slope is one, I think this is where the lowest point will be found. I think if you start with the lever horizontal, as high as it goes, when the
rope goes leftward and turns straight down, call Angle = zero.
Maybe a 3-D graph where angle goes back, but just view the resulting
2-D graph by viewing parallel to the angle axis.
So as the angle varies, delta-hypotenuse (from rope tiedown to pulley) at first
doesn't change much, but delta-y (distance pulley is from the top) changes fast at first.
You probably already are way past this, but thought I'd write my thoughts.
igloo myrtilles fourmis
Offline
#3 2007-02-23 15:58:45
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Marquis De L'Hopital optimization problem
Actually I change my mind, make the angle theta, the angle between the lever and the horizontal.
And to make easier, make the lever exactly one unit long.
Now also reason that the square of delta y and the square of delta hypotenuse will be equal at the lowest point.
Squared or not, we don't care, the numbers are the same, but it simplifies my equations.
Now y^2 = sin^2(theta).
And hyp^2 = (m + 1 - cos(theta))^2 + sin^2(theta).
So note the same terms in bold ink.
(Where "m" is the positive horizontal distance from rope pivot point leftward to pulley, just the x-component)
Last edited by John E. Franklin (2007-02-23 16:04:13)
igloo myrtilles fourmis
Offline
#4 2007-02-23 17:26:18
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Marquis De L'Hopital optimization problem
That didn't work, how about a new approach:
Maximize (y - hyp), or maximize (sinθ - squareRootOf{[m + 1 - cosθ]^2 + sin^2(θ) } )
igloo myrtilles fourmis
Offline
#5 2007-02-23 21:09:16
- fredekr
- Member
- Registered: 2007-02-20
- Posts: 5
Re: Marquis De L'Hopital optimization problem
I was going along those lines but I avoided the trig functions and stuck with Pythagoras.
I put it on a coordinate plane with the origin at the top left triangle vertex like so: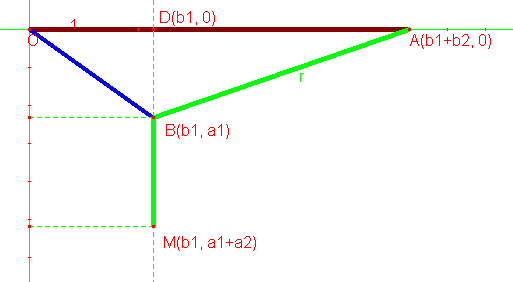
Them instead of focusing on the angle I focused on the point D. Either way will work of course.
So I got this to minimize (largest neg. value):
(for simplicity, let x=b1 from my diagram)
f(x) = sqrt(.16-x^2) + 1 - sqrt(-2x+1.16)
And my calculus is rusty but I could take the deriviative of f(x) but I think that f'(x) would be awful to solve symbolically. Of course we can plug f(x) into a numerical solver and get solutions, but that's not nearly as satisfying.
Offline
#6 2007-02-24 02:06:08
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Marquis De L'Hopital optimization problem
f(x) = sqrt(.16-x^2) + 1 - sqrt(-2x+1.16)
Starting with the above equation, I used the chain rule to differentiate it.
I too am rusty, but got:
1/2(.16-x^2)^-1/2(-2x) + 0 for the 1 above and - 1/2(-2x + 1.16)^-0.5(-2) = f ' (x)
Set to zero to get max or min.
Set to zero, put negative term on other side, cross-multiply...
Take the x outside of the square root and put it inside as x^2.
Square both sides to rid sqrt signs, is this okay to do???
I get 0 = 2x^3 - 2.16x^2 +.16
Now you need the zeros of a cubic. Not sure how to get them.
Last edited by John E. Franklin (2007-02-24 02:11:47)
igloo myrtilles fourmis
Offline
#7 2007-02-24 02:11:39
- bad_boi_aza1
- Member
- Registered: 2007-02-24
- Posts: 1
Re: Marquis De L'Hopital optimization problem
Hi
wotz ur name ?
Offline
#8 2007-02-24 02:15:08
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Marquis De L'Hopital optimization problem
Thanks for interrupting, aza, my name is John, don't trust everything I type, I'm trying to learn this stuff as I go. Was taught it many years ago though.
igloo myrtilles fourmis
Offline
#9 2007-02-26 23:29:18
- fredekr
- Member
- Registered: 2007-02-20
- Posts: 5
Re: Marquis De L'Hopital optimization problem
I get 0 = 2x^3 - 2.16x^2 +.16
Now you need the zeros of a cubic. Not sure how to get them.
From the graph of f'(x) we see that x=1 is a likely root. Use synthetic or polynomial division and verify that it is a root. Unfortunately f(1) doesn't make sense so we need to find other roots. From the division we have:
f'(x) = (x-1)(2x^2 - 0.16x - 0.16)
Then apply the quadratic, discard the nonsensical negative (discriminant) solution, leaving us
x = (0.16+sqrt(.0256+1.28))/4 ~= 0.326
and f(0.326) = .519 or 51.9 cm, which is indeed our solution.
Good work with the chain rule!
Best,
Kevin
Offline
Pages: 1