Math Is Fun Forum

shocamefromebay

Member

Registered: 2007-05-30

Posts: 103

square roots

can anyone figure this one out??? i can't, my teachers can't, my friends can't. none of my teachers can figure this out ro any of my friends and their teacehrs at any other school can either. any help or ideas? i know what the answer is, but i just don't know how to get there. can any one explain it to me? the answer is three minus the square root of three

Daniel123

Member

Registered: 2007-05-23

Posts: 663

Re: square roots

If anyone can work this out I will be very happy as well! It's really annoying me! Especialy as 67 and 37 are prime... ?

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: square roots

Now you have to find out why.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

Daniel123

Member

Registered: 2007-05-23

Posts: 663

Re: square roots

shocamefromebay has already told us the answer! and so has my calculator! but how do you do it?

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: square roots

Ah, didn't read the bottom of your post.  Simply square the whole thing, simplify, and take the square root.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: square roots

It might be important to note that square roots of irrational numbers of the form a + b√n can be found by:

(c + d√n)(c + d√n) = a + b√n

Or rather:

(c² + n*d²) + (2cd)√n

So: a = c² + d² and b = 2cd

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

shocamefromebay

Member

Registered: 2007-05-30

Posts: 103

Re: square roots

yea i did square the whole thing. it doesnt simplifiy. try it. its not taht simple. if it was, i wouldnt have posted this.

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: square roots

Certainly it does.  But there is an easier way.

So a = 1, 2, 4, 8, b = 1, 2, 4, 8.  You can pretty easily find that a = 8 and b = 1.  Thus:

Now apply the same idea to the right side.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: square roots

This would be an interesting application of algebraic number theory.  I just wish I knew more of it so I actually could...

I say this because I *think* that if c^2 + d^2 = a and 2cd = b does not have an integer solution, then it must have an irrational solution and this would mean that the number can not be simplified.  But this is just intuition, I have no idea if its right.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

shocamefromebay

Member

Registered: 2007-05-30

Posts: 103

Re: square roots

uhhhhh... yea. i have totally no idea what u just did. i squared it and got this 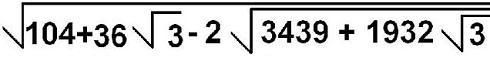i understood almost what u did in that first one with how u found the formula for the square root of 67 +16 sqquare root 3, but how did u get the possible values for a and b???and taht second post about uhhh that algebraic number theory. im not even gonna try to mess with that. i have no idea what that is. but how did u get the values for a and b??also, how did u find the answer to it the problem w/o readin what the answer was?did u use a ti 89??or somethign??

Last edited by shocamefromebay (2007-05-30 10:05:11)

mathsyperson

Moderator

Registered: 2005-06-22

Posts: 4,900

Re: square roots

He's just worked out what each square root is. He's guessed that it will be in the form a + b√3, and then squared that to get the simultaneous equations.

(a+b√3)² = a² + 2ab√3 + 3b².
∴ a² + 3b² = 67; 2ab = 16.

That solves to give 8 + √3, and the other one solves to give 5 + 2√3.
Subtract the second from the first, and you have your answer.

Very nice method by the way, Ricky. I was thinking along the lines of squaring the whole thing, and it was just getting more and more icky.

---

Why did the vector cross the road?
It wanted to be normal.

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: square roots

And let me be more explicit with what I said in my last post.  I assumed I will get integer solutions, then went looking for them.  This is because I believe that if I don't get integer solutions, then I must get irrational ones, in which case it wouldn't be simplified.  Again, it is a belief, and I intend on proving it shortly, just not tonight.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

John E. Franklin

Member

Registered: 2005-08-29

Posts: 3,588

Re: square roots

Try multiplying (5+2√3) times itself.  Surprise!!
25 + 12 + 20√3
I just kept guessing until I found it!!

---

igloo myrtilles fourmis

shocamefromebay

Member

Registered: 2007-05-30

Posts: 103

Re: square roots

OO i get it now. but how do u do it when u square and simplify it?

John E. Franklin

Member

Registered: 2005-08-29

Posts: 3,588

Re: square roots

Well... (8 + √3) - (5 + 2√3)
        8 - 5 + √3 - 2√3
         3    -  √3

---

igloo myrtilles fourmis

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: square roots

OO i get it now. but how do u do it when u square and simplify it?

I was hoping you weren't going to ask this... When I first did it, I squared it, then used this method to simplify.  Afterwards, I realized that this method could be applied directly and squaring it was not only pointless, it made the whole thing more complex.  What can I say, it was pretty irrational on my part.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."