Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2007-08-14 21:55:02
- Hastega
- Member
- Registered: 2007-06-20
- Posts: 7
Help! Integral Calculus
Can someone help me with these two problems?
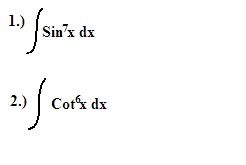
Offline
#2 2007-08-15 00:05:41
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: Help! Integral Calculus
According to Wikipedia table of integrals:
but it didnt have anything for cotangent.
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#3 2007-08-15 01:15:57
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: Help! Integral Calculus
Possibly split the cotangent into sine and cosine, then use integration by parts? Just a guess.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#4 2007-08-15 04:09:57
- HallsofIvy
- Guest
Re: Help! Integral Calculus
The first is an easy "standard" problem because it has sine to an ODD power.
Write it as int sin^6(x) (sin(x)dx) = int (1- cos^2(x)^3 (sin(x)dx). Now let u= cos(x) so that du= -sin(x)dx and we have -int (1- u^2)^3 du= -int (1- 3u^2+ 3u^4- u^6)du= -(u- u^3+ (3/5)u^5- (1/7)u^7)+ C= (1/7)cos^7(x)-(3/5)cos^5(x)+ cos^3(x)- cos(x)+ C.
I'm surprised Wikipedia doesn't have such a formula for cot. My Calculus book gives
int cot^n (x)dx= - (cot^(n-1)(x))/(n-1)- int cot^(n-2)(x)dx.
#5 2007-08-15 20:02:27
- Hastega
- Member
- Registered: 2007-06-20
- Posts: 7
Re: Help! Integral Calculus
So (1/7)cos^7(x)-(3/5)cos^5(x)+ cos^3(x)- cos(x)+ C is the answer to number 1.
I believe the formula for Cot is 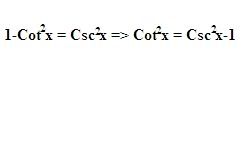
But i still can't answer it, I always get stuck because there not integrable.
Offline
#6 2007-08-15 20:30:31
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: Help! Integral Calculus
for 1 i get:
which according wolfram integrator can be simplified to:
Last edited by luca-deltodesco (2007-08-15 20:33:36)
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#7 2007-08-16 01:09:07
- gnitsuk
- Member

- Registered: 2006-02-09
- Posts: 121
Re: Help! Integral Calculus
Problem 2:
To solve this we need only the basic result:
Which is easily obtained via the trig relation:
For then:
for n >= 2.
(Which is the formula metioned by HallsofIvy)
So we can always reduce to the case n = 1 or n = 0.
This will allow you to solve the given integral.
Last edited by gnitsuk (2007-08-20 20:57:54)
Offline
Pages: 1