Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#26 Re: Help Me ! » Circle in an angle » 2022-11-01 10:21:25
This time we seem to have more or less the same approach.
You took O for origin, C for center and A for angle ?
The basic trigonometry formulas:
sin(alpha)=opposite/hypotenuse
cos(alpha)=adjacent/hypotenuse
tan(alpha)=opposite/adjacent
cot(alpha)=adjacent/opposite
(cause of the numerator/denominator flip
the 4th is not very worn out.)
In Germany, we often remember this
with somewhat funny abbreviations.
GAGA (=> crazy)
--------- (fraction line)
HHAG (Hummel Hummel AG => working like a bee, working like a bee - semi-public enterprise)
G => opposite.
A => adjacent
H => hypotenuse
With this you have those fractions after the equal sign.
The order sine, cosine, tangent cotangent needs to be
remembered by rote learning, here.
How is it being done in the UK ?
Now the trigonometry:
O->C:
sin(a)=G/H
H=G/sin(a)
H=r/sin(a/2)
O->A:
tan(a)=G/A
A=G/tan(a)
A=r/tan(a/2)
Edit: Correcting mistake.
#27 Re: Help Me ! » Find Domain of f(x) » 2022-10-30 10:26:42
You could look at the function graph and see if it helps you ;-)
Now let's look at the equation:
x² does always yield positives. even if you set x to a negative.
Could this already be the reason ?
Further its always even and x²+1 is always uneven.
Taking the root of positives gives you real numbers
(as opposed to imaginary numbers if you take it from a negative).
Cause of the +1,
1 would be the smallest number, you would have in the root.
1 times 1 is 1, so the square root of 1 equals 1.
5/1 equals 5.
Since there is no shifting, the numerator,
in this case 5, is the y-Intercept here.
So much for now.
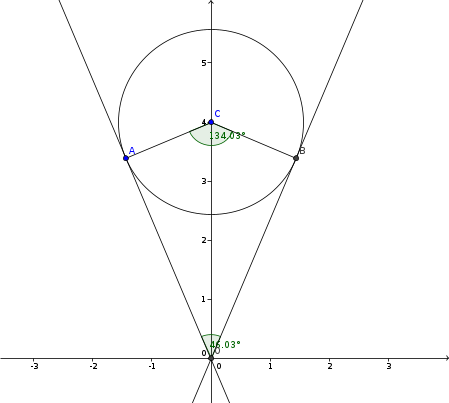
#28 Help Me ! » Circle in an angle » 2022-10-30 08:43:12
- mathdrop
- Replies: 2
This is supposed to be a simpler 2D version
of a ball/torus resting in the tip of a pyramid.
It is about a circle resting in an angle.
Relative to the corner of the angle:
Where is the center of the Circle ?
Where does the Circle touch the angle ?
#29 Re: Help Me ! » Circle on hyperbola » 2022-10-30 02:13:23
It would be nice, if you could try to show me
the right y for a given x (q and p in your example),
with specific number pickings.
As a test, I would also run your numbers
through the approximate procedure,
which I outlined in my second post in this thread.
So, let's go ;-)
#30 Re: Help Me ! » Circle on circle » 2022-10-30 01:01:54
Please tell me, how you get to equation number 3
and the unlabelled one just before.
#31 Maths Is Fun - Suggestions and Comments » Geometry upload » 2022-10-29 06:04:03
- mathdrop
- Replies: 0
In my post about a ball/torus resting in the tip of a pyramid,
I had some excerpts out of a CAD file.
What about a possibility to upload such files ?
#32 Maths Is Fun - Suggestions and Comments » Posting without referrer headers possible ? » 2022-10-27 09:59:53
- mathdrop
- Replies: 4
As already mentioned while introducing me,
your forum requires a referrer header for posting.
If I happen to not send them,
this means I have to activate them in my browser,
post my message, and then deactivate them again.
I do not know yet if FluxBB would in general work
without referrer headers, but if so,
would you please be so kind and switch them of ?
#33 Re: Help Me ! » Circle on circle » 2022-10-27 09:10:03
There are 4 cases
in which the circles have one point
(same slope, there) in common.
Your graph depicts the first one.
If you move the little circle along the line,
you get the other cases.
I particularly thought of the third one,
but it should not make much difference,
mathematically.
Please describe in more detail,
what you are doing after the two circle equations.
#34 Re: Help Me ! » Circle on hyperbola » 2022-10-27 00:40:44
You nailed the graph :-)
(One could consider, if one wants the radius of the circle
to be the same as in the apex of the hyperbola (called vertex),
but this is not fix and thus not required.
However, a bigger circle is limiting the range of the x-shifting.)
As you can see, I'm still trying
to improve making me understood ;-)
But it might be worth while, so of it is bearable,
I would probably go on with that for a while.
Nice Drawings, by the way.
Which Software do you use ?
Is there something comparable in Linux ?
I do not have B and just the x-value of A.
I however have the radius an thus
the distance between A and B.
I also have the hyperbola.
The y-value of A should be wherever he circle
has one single point in common with the hyperbola,
on which it also shares the same slope with the hyperbola.
For r_circle<=r_vertex:
If one would roll the ball trough the ditch,
its center would draw another hyperbola, right ?
#35 Help Me ! » Circle on circle » 2022-10-18 10:29:29
- mathdrop
- Replies: 9
This is about intersecting a circle with another of different size
in on point in which both circles have the same slope.
Starting with the equation of a circle x²+y²=r² <=> y=sqrt(r²-x²).
Adding variables for shifting
(a for the x direction and b for the y direction):
(x−a)²+(y−b)²=r²
Solving it for y:
y = +/- sqrt(-a²+2*a*x+r²-x²)+b
The first derivative:
d/dx(sqrt(-a²+2*a*x+r²-x²)+b)=(a-x)/sqrt(-a²+2*a*x+r²-x²)
For the second circle: c=a2, d=b2, q=r2.
For the intersection point, this gives us the following equation system;
sqrt(-a²+2*a*x+r²-x²)+b=sqrt(-c²+2*c*x+q²-x²)+d
(a-x)/sqrt(-a²+2*a*x+r²-x²)=(c-x)/sqrt(-c²+2*c*x+q²-x²)
If we define the position of the second circle,
and their sizes, and only shift horizontally,
we still have a and x variable.
Am I on the right track,
and if so, Is there something wrong,
since we only have 2 equations here ?
Edit:
The centers of the circles and the intersection
are on the same line when the slopes match.
Maybe something could be done with that.
#36 Re: Help Me ! » Circle on hyperbola » 2022-10-18 07:30:04
Thank you, Bob :-)
We take your initial choice
and flip the circle to the inside of the hyperbola,
so it resembles a ball in a ditch.
Now we push it a little uphill and freeze.
What is it's Y-Value ?
Edit: Being more specific.
#37 Re: Help Me ! » Circle on hyperbola » 2022-09-18 14:38:58
It is that my PC was a little sketchy, using my approach,
But since there were no other suggestions,
I guess I will go down that route.
So, Imagine the friendly circle sitting peacefully on the arm of the hyperbola.
Now, let's see if it would help, if we draw a triangle into it.
It's hypotenuse goes from the center of the circle A
to the intersection with the hyperbola B.
Moving horizontally over B gives us C.
The hypotenuse is always perpendicular
to the slope of the hyperbola in point B
and the angle on A is just angle=atan(slope in B).
The above enables us to put an approximate procedure.
For getting the first test value,
I use the angle of the hyperbolas asymptotes (e.g. at 45°).
I use trigonometry to get the x value.
Then I check what slope the hyperbola at that x-value has
and convert it to an angle. It will be flatter.
Than I again use trigonometry to get the x value. And so forth.
This should converge to the desired x value
in ever smaller steps.
If the (angle)change falls under a certain threshold,
I stop it and take the value.
So much for now. Maybe later some more details and stuff.
Edit: I called a point wrong; "under A" => "over B" (complementary angle meant before)
#38 Help Me ! » Circle on hyperbola » 2022-05-06 15:03:48
- mathdrop
- Replies: 22
This is about putting a circle on top of a hyperbola
(a*sqrt(b^2+x^2))/b, where a = semi major axis and b = semi minor axis,
so that they have one point in common,
while the center of the circle matches, or is close to, a given x.
How to do it ?
#39 Re: Help Me ! » Linking two Bézier curves » 2022-05-04 22:31:56
What is the source of the answer, you have got ?
May you tell us something about the problem, you are trying to solve ?
For instance with a qubic spline,
you could just give the points A, C, E and B, D would not be an issue.
Do you need B ?
#40 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-05-03 15:53:25
Without you motivating me,
I probably wouldn't have solved this yet.
Something I might add:
Till here it worked on paper, but for using it with my computer,
I was putting back the floor plus, in the torus planes edged, balls trough it,
so that their center is in the floor plane.
This by shifting the 2 planes next to the edges, one of which the torus lies flat on,
with the floor plane by the radius of the ball.
Cutting the planes in each of the 2 cases gives unique points.
Instead of with the lines, coming out of the equation systems,
I defined the vectors, which intersect the core of the torus
using the balls in combination width the one on the tip.
This way I avoided an underdetermined bosl2 solve,
resulting in the minimum norm solution (point on line, closest to origin).
It made sure, that the vectors always point in the right direction.
Edit: Being more specific
#41 Re: Help Me ! » how do we use math in everyday life » 2022-05-03 15:10:30
The math we have discovered yet is finite,
and there are maybe a bunch of people like my,
who have been able to make use of a lot of it.
Of course it depends on your everyday life
and how you choose it to be.
With math, you could, for instance,
create soundwaves or models of 3D-Objects
(look at the shapes of all the parts,
you have in your household or a car).
And so much more..
You can tackle stuff you would not even have imagined,
but maybe you will miss some life out there, while looking
on a piece of paper or nowadays a computer screen.
#42 Dark Discussions at Cafe Infinity » The human behind » 2022-05-03 14:27:48
- mathdrop
- Replies: 0
We humans, who discovered all those relations,
are very fragile in nature.
Health is the enabling factor, which makes math possible.
The brain does not feed on math exercises, believe it or not.
It feeds on oxygen, food and water.
So, being able to get exercises without being able to get information
on how to keep the body, especially the brain, healthy,
might be a little one-sided, don't you think ?
I've even met math teachers who have lost their skills.
Humans are not math robots, that should not be forgotten.
#43 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-03-25 10:46:18
It seems, that I got it sorted, too.
Mainly I did like I described above.
Before the torus I dropped a ball with its rounding as radius.
Its center gives you the displacement due to shifting.
Not to forget to tip an turn the radius.
It's just the dot product used with
unit vectors in direction of the axes (e.g. z and y)
and the normal vector of the plain
on which the torus rests flat.
Edit: putting z and y instead of z and x.
#44 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-03-25 01:41:29
What about the torus ?
#45 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-03-15 10:56:46
Since I had some faults there,
I checked if it works with displacement vectors,
and it does.
One should not forget to add the dot-products
of the cross-products and the displacement vectors
divided by their length's
to the right side of the solution grid, here.
My OpenSCAD code does also render it correctly
(I have been using the BOSL2 library, cause solve):
use <~/.local/share/OpenSCAD/libraries/bosl2/std.scad> // linear_solve
module spherepolyhedron(corners)
{
module cornerput(corner)
{
//[[x,y,z],[[x,y,z],[x,y,z]],[[x,y,z],[x,y,z]],[[x,y,z],[x,y,z]],r_sphere]
tip=corner[0];
plainp=[[corner[1][0],corner[1][1]], // plainp(oints)
[corner[2][0],corner[2][1]],
[corner[3][0],corner[3][1]]];
r_sphere=corner[4];
plainv=[[plainp[0][0]-tip,plainp[0][1]-tip], // plainv(ectors)
[plainp[1][0]-tip,plainp[1][1]-tip],
[plainp[2][0]-tip,plainp[2][1]-tip]];
crossp=[cross(plainv[0][0],plainv[0][1]), // crossproducts
cross(plainv[1][0],plainv[1][1]), // zero if vector=0 or paralell
cross(plainv[2][0],plainv[2][1])];
vleng=[norm(crossp[0]), // vectorlength's
norm(crossp[1]),
norm(crossp[2])];
nlizedv=[crossp[0]/vleng[0], // normalized vectors
crossp[1]/vleng[1], // crossp=0 produces X/0 -> nan here
crossp[2]/vleng[2]];
matrix=nlizedv;
vector=[crossp[0]*tip/vleng[0]+r_sphere,
crossp[1]*tip/vleng[1]+r_sphere,
crossp[2]*tip/vleng[2]+r_sphere];
pos=linear_solve(matrix,vector); // bosl2 library
translate(pos)
sphere(r_sphere);
}
for(corner=corners)
cornerput(corner);
}
spherepolyhedron( // the points i have defined before
[[[0,0,0],[[2,0,1],[0,2,1]],[[0,1,1],[-1,0,1]],[[-2,-3,1],[2,-3,1]],.5]]);
*spherepolyhedron( // centerpoints of spheres in the edges of a unit cube
[[[0,0,0],[[0,0,1],[1,0,0]],[[0,1,0],[0,0,1]],[[1,0,0],[0,1,0]],.05],
[[1,0,0],[[0,0,0],[1,0,1]],[[1,0,1],[1,1,0]],[[1,1,0],[0,0,0]],.05],
[[1,1,0],[[1,0,0],[1,1,1]],[[1,1,1],[0,1,0]],[[0,1,0],[1,0,0]],.05],
[[0,1,0],[[1,1,0],[0,1,1]],[[0,1,1],[0,0,0]],[[0,0,0],[1,1,0]],.05],
[[0,0,1],[[1,0,1],[0,0,0]],[[0,0,0],[0,1,1]],[[0,1,1],[1,0,1]],.05],
[[1,0,1],[[1,0,0],[0,0,1]],[[0,0,1],[1,1,1]],[[1,1,1],[1,0,0]],.05],
[[1,1,1],[[1,1,0],[1,0,1]],[[1,0,1],[0,1,1]],[[0,1,1],[1,1,0]],.05],
[[0,1,1],[[0,1,0],[1,1,1]],[[1,1,1],[0,0,1]],[[0,0,1],[0,1,0]],.05]]);Edit: Linking OpenSCAD page.
#46 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-03-14 03:32:38
Thank's for explaining.
Regarding the order in which I took the points above the origin,
I followed no rule, therefore some normal vectors pointed in the wrong direction.
Some mistakes later, I took the right hand rule
(for this I made multiple edits of this post,
to avoid posting a bunch of my mistakes
and therefore possible confusion).
Starting all over.
This time with the same numbers
except I flipped B2 and B3 as well as C2 and C3 for correctly
using the left hand rule, so the normal vector should point inwards,
into or through the (upside down irregular triangular) pyramid:
Here, the first point in every plain
is the origin=A1=B1=C1=0v=the v(ector) 0 .
Points:
A1=(0|0|0), A2=(2|0|1), A3=(0|2|1)
B1=(0|0|0), B2=(0|1|1), B3=(-1|0|1)
C1=(0|0|0), C2=(-2|-3|1), C3=(2|-3|1)
A1A2=A2-A1=A2 and so on.
Therefore:
A:x=r*A2+s*A3=r*(2|0|1)+s*(0|2|1) and so on (see post 4 except flipped).
Doing the cross product for getting the normal vectors n:
A2 X A3 = (2|0|1) X (0|2|1) = (0*1-1*2|1*0-2*1|2*2-0*0) = (-2|-2|4)
B2 X B3 = (1|-1|1)
C2 X C3 = (0|4|12)
Taking the length's |n| of the vectors n for the Hesse stuff later:
|(-2|-2|4)|=sqrt((-2²)+(-2²)+4²)=sqrt(4+4+16)=sqrt(24)
|(1|-1|1)|=sqrt(3)
|(0|4|12)|=sqrt(160)
The normal form:
A:(-2|-2|4)*(x-0v) and on.
Multiplying this out to get the Cartesian form:
(-2|-2|4)*(x|y|z)-(-2|-2|4)*(0|0|0)=0 and on.
Normalizing following Hesse:
A:-2x-2y+4z=0 -2x-2y+4z/sqrt(24)=0
B:x-y+z=0 x-y+z/sqrt(3)=0
C:4y+12z=0 4y+12z/sqrt(160)=0
Since I figured, that I can jump over the Hesse form,
like you portrayed it, I have not even looked up,
how to get there again. How, by the way ?
The 3 planes have a single point in common.
Since they all touch the sphere, it is in its center,
if they are shifted towards there by the radius of the sphere:
A:(-2x-2y+4z)/sqrt(24)=0.5=radius of sphere/sqrt(24)
B:(x-y+z)/sqrt(3)=0.5=radius of sphere/sqrt(3)
C:(4y+12z)/sqrt(160)=0.5=radius of sphere/sqrt(160)
I brought it in this solve grid:
2/sqrt(24) |2/sqrt(24) |-4/sqrt(24) 0.5
[1/sqrt(3) |-1/sqrt(3) |1/sqrt(3) ] = [ 0.5 ]
0/sqrt(160)|4/sqrt(160)|12/sqrt(160) 0.5
From there or from
solve([(-2x-2y+4z)/sqrt(24)=0.5, (x-y+z)/sqrt(3)=0.5, (4y+12z)/sqrt(160)=0.5],[x,y,z])
I've let the computer take over (equal results).
Now it gives me:
center of sphere
= ((1/18)*(5*sqrt(3)-4*sqrt(6)+sqrt(10)) | (1/6)*(-sqrt(3)-sqrt(6)+sqrt(10)) | (1/18)*(sqrt(3)+sqrt(6)+2*sqrt(10)))
≈ (0.11248 | -0.16988 | 0.58367)
Is there something left to explain in more detail ?
Would it work, with displacement vectors included in the plains, accordingly ?
Would it make sense to adapt our definitions somehow,
so that our models represent similar scenes ?
Edit's to avoid confusion: Using the right hand rule, so flipping B2 and B3, C2 and C3 (see beginning of post).
#48 This is Cool » Curvature of hyperbola » 2022-03-11 09:27:09
- mathdrop
- Replies: 0
Give me the curvature of xy=1 in every point.
Why can't we take the second derivative of it ?
My solution would probably be to rotate it 45° counter-clockwise,
take the second derivative
find the relation it has with the unaltered equation
and transform it back.
Is there something out there, which is more handy ?
#49 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-03-11 04:50:37
One could calculate the angle
between the two intersection vectors, which touch the core of the torus
(and divide it by 2 for getting an angle of said triangle).
Then one could use trigonometry for calculating the coordinates of its center.
Is this the easiest way ?
#50 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-03-11 04:13:15
Taking on the torus:
Similar to how I made the 3 planes meet at the center of the circle:
One could slice the torus horizontally with (the second) plane, on which it lies flat.
One could slice the core circle with the other planes (we probably need just one).
The intersection of those gives us a vector, which touches the core of the torus
(due to the shifting, it does not necessarily go trough the origin).
There it is perpendicular.
Since we just have the radius and no other distance/angle,
we probably can not go straight for trigonometry at this point.
The unused plane probably wouldn't be of any help, too, or would it ?
Any ideas ? :-)