Math Is Fun Forum

mikau

Member

Registered: 2005-08-22

Posts: 1,504

need a geometry reminder

if we are given the triangle in the attached diagram, and we know the ration of a/b, does that tell give us any equations relating L1, L2, and L3?

---

A logarithm is just a misspelled algorithm.

mikau

Member

Registered: 2005-08-22

Posts: 1,504

Re: need a geometry reminder

does no one remember any sort of proportionality relation for this? I could have sworn there was one.

---

A logarithm is just a misspelled algorithm.

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: need a geometry reminder

Wouldn't you just make it into a right triangle and then use trig functions, the leg of the left triangle being of length L?

Edit: #3000

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

mikau

Member

Registered: 2005-08-22

Posts: 1,504

Re: need a geometry reminder

Congrats on 3000 posts!

But I'm not sure I follow you. You mean draw a line straight down from the upper left vertex, and  extend the base line leftward to meet it?

---

A logarithm is just a misspelled algorithm.

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: need a geometry reminder

Yes, label the vertical extension L and the horizontal extension K.  So the length of the horizontal extension plus a is K+a, and similarly with K+b.  Then we have:

I'll work on this later when I get home, but it should be all algebra from here.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

krassi_holmz

Real Member

Registered: 2005-12-02

Posts: 1,905

Re: need a geometry reminder

The proble is that a/b, not a and b. On the other hand, if there are given all the elements exept 1, you can find it by solving one of the little triangles...

---

IPBLE:  Increasing Performance By Lowering Expectations.

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: need a geometry reminder

Given a and b (not just a/b), there is no way to relate them.  We may prove this by showing that constant a and b will allow for two different relations between L1 and L2.

Proof: Let a = b, both nonzero, and p be the point where the segment of length a and b meet.  Now assume that L2 is orthogonal to the segments of length a and b.  Then we have that L1 = L3 (since a = b) by SAS, the angle being the 90 degree angle between the two orthogonal segments.

Now keeping a = b, let L2 lie on the line defined by extending the segments of length a and b in both directions.  We now see that L1 + a + b = L3.

Therefore, with constant a and b we have that L3 = L1 or L3 = L1 + a + b.  Thus, there is no way to relate them as a function in terms of a and b.  (i.e. this function would not be well-defined).

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

krassi_holmz

Real Member

Registered: 2005-12-02

Posts: 1,905

Re: need a geometry reminder

Given a and b (not just a/b), there is no way to relate them.

I wanted to say given all of L1, L2, L3, a, b, except 1 of them.

---

IPBLE:  Increasing Performance By Lowering Expectations.

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: need a geometry reminder

The proof of mine above is wrong.  It can very quickly be saved by stating that in both of the conditions L2 was also held constant.

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

mikau

Member

Registered: 2005-08-22

Posts: 1,504

Re: need a geometry reminder

thanks for the replies, and the interesting discussion!

fortunately I found a relation between L1, L2 and L3, but only if you consider them as vectors.

consider the points A,B,C and Q and the scaler k defined as below: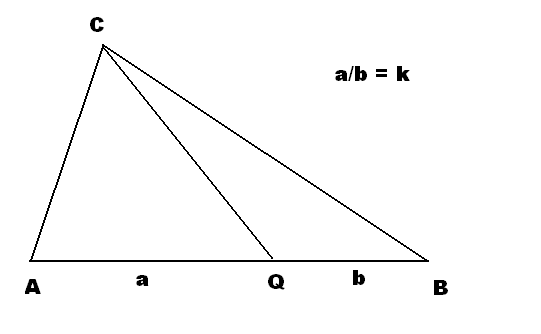

obviously,,

and

and observe:

so

thus multiplying equation (2) by k and adding the result to equation (1), and solving for (C-Q) yields

not exactly the problem i asked initially, but it gives me the sort of relation i wanted.

Last edited by mikau (2008-09-11 10:35:17)

---

A logarithm is just a misspelled algorithm.