Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2008-09-07 12:11:08
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
need a geometry reminder
if we are given the triangle in the attached diagram, and we know the ration of a/b, does that tell give us any equations relating L1, L2, and L3?
A logarithm is just a misspelled algorithm.
Offline
#2 2008-09-09 07:07:03
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: need a geometry reminder
does no one remember any sort of proportionality relation for this? I could have sworn there was one.
A logarithm is just a misspelled algorithm.
Offline
#3 2008-09-09 13:57:59
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: need a geometry reminder
Wouldn't you just make it into a right triangle and then use trig functions, the leg of the left triangle being of length L?
Edit: #3000
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#4 2008-09-09 23:37:12
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: need a geometry reminder
Congrats on 3000 posts! ![]()
But I'm not sure I follow you. You mean draw a line straight down from the upper left vertex, and extend the base line leftward to meet it?
A logarithm is just a misspelled algorithm.
Offline
#5 2008-09-10 05:15:01
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: need a geometry reminder
Yes, label the vertical extension L and the horizontal extension K. So the length of the horizontal extension plus a is K+a, and similarly with K+b. Then we have:
I'll work on this later when I get home, but it should be all algebra from here.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#6 2008-09-10 09:20:22
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: need a geometry reminder
The proble is that a/b, not a and b. On the other hand, if there are given all the elements exept 1, you can find it by solving one of the little triangles...
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#7 2008-09-10 10:05:05
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: need a geometry reminder
Given a and b (not just a/b), there is no way to relate them. We may prove this by showing that constant a and b will allow for two different relations between L1 and L2.
Proof: Let a = b, both nonzero, and p be the point where the segment of length a and b meet. Now assume that L2 is orthogonal to the segments of length a and b. Then we have that L1 = L3 (since a = b) by SAS, the angle being the 90 degree angle between the two orthogonal segments.
Now keeping a = b, let L2 lie on the line defined by extending the segments of length a and b in both directions. We now see that L1 + a + b = L3.
Therefore, with constant a and b we have that L3 = L1 or L3 = L1 + a + b. Thus, there is no way to relate them as a function in terms of a and b. (i.e. this function would not be well-defined).
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#8 2008-09-10 10:30:10
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: need a geometry reminder
Given a and b (not just a/b), there is no way to relate them.
I wanted to say given all of L1, L2, L3, a, b, except 1 of them.
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#9 2008-09-10 10:36:39
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: need a geometry reminder
The proof of mine above is wrong. It can very quickly be saved by stating that in both of the conditions L2 was also held constant.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#10 2008-09-11 10:21:17
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: need a geometry reminder
thanks for the replies, and the interesting discussion! ![]()
fortunately I found a relation between L1, L2 and L3, but only if you consider them as vectors.
consider the points A,B,C and Q and the scaler k defined as below: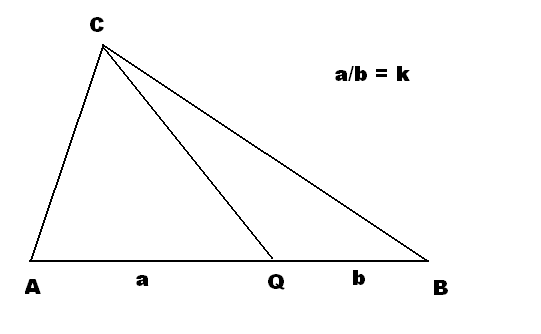
obviously,,
and
and observe:
so
thus multiplying equation (2) by k and adding the result to equation (1), and solving for (C-Q) yields
not exactly the problem i asked initially, but it gives me the sort of relation i wanted.
Last edited by mikau (2008-09-11 10:35:17)
A logarithm is just a misspelled algorithm.
Offline
Pages: 1