Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: Help Me ! » Algebraic equation-system describing a horn-antenna » 2023-05-07 02:06:55
The lecturer referenced a book from which I may get solutions,
but not the detailed steps originating from the equations above.
It seems to be hard to get there, so I'll first with that for now.
#2 Help Me ! » Algebraic equation-system describing a horn-antenna » 2023-05-05 13:33:44
- mathdrop
- Replies: 1
After following the lecture about horn-antennas,
I was was stuck with the equation system,
so I could not do the example of the lecturer.
It could well come down to forgotten solving techniques
and I would be happy if someone could fix me ;-)
Since I'm not used to latex, I redefine as follows:
Knowns:
c=a=0.02286m // (horizontal) waveguide aperture in H-field-direction
d=b=0.01016m // (vertical) waveguide aperture in E-field-direction
l=lambda=0.03m // wavelength
f=D=20db=100dimensionless // directivity
n=51%=0.51 // aperture efficiency
Unknowns:
a=A // (horizontal) aperture in H-field-direction
b=B // (vertical) aperture in E-field direction
g=R1 // r min in the H-plane
h=R2 // r min in the E-plane
j=RH // flare-height in H-field-direction
k=RE // flare-height in E-field direction
s=lH // slant-height in H-field-direction
t=lE // slant-height in E-field direction
Set of equations:
f=4*pi/l^2*n*A // out of antenna theory
A=a*b // A=aperture area
s^2=g^2+(a/2)^2 // Pythagoras geometry
t^2=h^2+(b/2)^2 // Pythagoras geometry
j/g=(a-c)/a // triangle parallel cut
k/h=(b-d)/b // triangle parallel cut
j=k // horn has a flat front edge
s-g=.375*l // flare angle in H-direction
t-h=.25*l // flare angle in E-direction
I rearranged the equations a little
and did basic stuff:
f=4*pi/l^2*n*a*b // 1, A->a*b since A=a*b
<=> a*b=f/(4*pi/l^2*n)
<=> a*b=f*l^2/(4*pi*n)
<=> b=f*l^2/(4*pi*n*a)
s^2=g^2+(a/2)^2 // 2
<=> a=2*sqrt(s^2-g^2)
t^2=h^2+(b/2)^2 // 3
<=> b=2*sqrt(t^2-h^2)
<=> h=sqrt(4*t^2-b^2)/2
k/g=(a-c)/a // 4, j->k since j=k
<=> k=g-(c*g)/a
k/h=(b-d)/b // 5
<=> h=(b*k)/(b-d)
s-g=.375*l <=> s=.375*l+g // 6
t-h=.25*l <=> t=.25*l+h // 7
Then I tried to solve for b, first:
h=(b*(g-(c*g)/a))/(b-d) // 4 in 5, eliminating k
<=> (b*g*(a-c))/(a*(b-d))
Now there are many variables, shared by many equations.
Therefore I had trouble using the eliminating approach.
How could I proceed ?
#3 Re: Help Me ! » What is the best way to understand division » 2023-03-26 17:32:30
10 / 1/2 = 10/1 / 1/2 = 10/1 * 2/1 = 10*2 = 20 if i'm right.
in general, Frank Cardulla, a teacher at the niles north high school in a chicago suburb,
said: by dividing you make the denominator 1.
he made high school chemistry video lectures,
in which he also explained a lot of math
(i would recommend the first edition, where he was younger,
but i can only find the second advert removed.
unfortunately they are ttc videos, which are not free.
#4 Re: Help Me ! » Inequalities basics » 2023-02-24 10:14:33
#5 Re: Help Me ! » Reflecting point on plane through origin » 2023-02-21 11:26:01
That's, what I needed.
Now I'll go refreshing my memory about the single steps.
(The point is anywhere in 3D.)
#6 Re: Help Me ! » Intersecting a graph with a line in 3d » 2023-02-20 12:02:41
3*x^4=1 where x=y=z
x=y=z=+/- 1/3^(1/4)≈+/- 0.75984
Your point hits the shape :-)
How have you gotten 3*x^4=1 ?
I moved everything to one side:
x^4+y^4+z^4-1=0
f*x+f*y+f*z-r=0
Set them equal:
x^4+y^4+z^4-1=f*x+f*y+f*z-r
And tried to solve the above for x,
but this gave me wild formulas.
#7 Help Me ! » Reflecting point on plane through origin » 2023-02-20 04:42:38
- mathdrop
- Replies: 2
I have the normal vector of a reflection-plane which goes through the origin.
How to reflect a point on this plane ?
#8 Re: Help Me ! » Circle on circle » 2023-02-20 03:52:17
There is a geometric solution.
This one is by moving the big circle down the y-axis, till they touch.
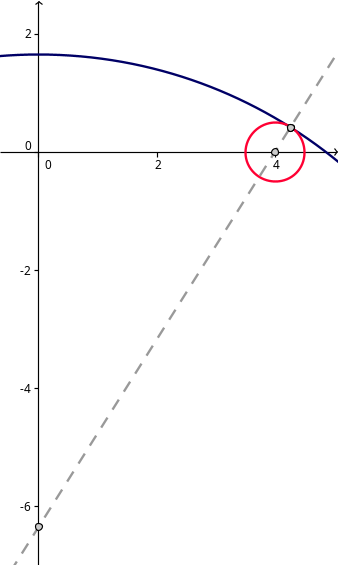
I'm still not entirely sure if I can not use calculus,
having 2 shifted circles, one with a free variable,
and finding the shift so they have one point in common, and why.
Maybe I should have taken derivatives in post 7 like so:
y=b +/- sqrt(-a^2+2*a*x+r^2-x^2)
y'=(+/- a -/+ x)/sqrt(-a^2+2*a*x+r^2-x^2)
y=d +/- sqrt(-c^2+2*c*x+s^2-x^2)
y'=(+/- c -/+ x)/sqrt(-c^2+2*c*x+s^2-x^2)
(a-x)/sqrt(-a^2+2*a*x+r^2-x^2)-y=(c-x)/sqrt(-c^2+2*c*x+s^2-x^2)-y
<=>
(a-x)/sqrt(-(a-r-x)*(a+r-x))+(x-c)/sqrt(-(c-s-x)*(c+s-x))=0
a=+/- (c*r-r*x+s*x)/s
c=+/- (a*s+r*x-s*x)/r
This seems to be solved now.
Just with the derivatives (slopes) I can just use horizontal shifting,
because they do not contain values for vertical shifting.
If needed, I probably could work around or use another approach, here.
In the geometric example I could have as well moved the little circle to the right.
#9 Help Me ! » Torus projection » 2023-02-15 00:30:05
- mathdrop
- Replies: 0
I'm after the equations of the projection
of a rotated torus on the xy-plane.
Imagine you have a donut,
which is shaped like a torus.
Now you symetrically poke it on a stick,
so the stick goes twice through the donut.
You place the stick before the x-axis and rotate it
with a light source before it.
See the borders of the shadow of the donut ?
I would like to find the equations of them.
If the donut is paralel to the xy-plane, you have 2 circles.
One bigger and one smaller.
If the donut is paralell to the xz-plane, you have 1 circle,
cut, pulled apart along x and a rectangle in between.
What if the donut is rotated by 45° ?
What if the donut is rotated by another angle ?
@Bob:
Thank you for helping me with the sphube-line intersection.
I would need some more time, there.
#10 Help Me ! » Intersecting a graph with a line in 3d » 2023-01-18 06:52:42
- mathdrop
- Replies: 3
I would like to intersect the function y=(a^n-x^n-z^n)^(1/n),
which describes a sphube, being a rounded cube with its center in the origin,
with the line, going trough the origin and P=(1|1|1).
I tried it with y=x+z and y=3-x-z,
but the computer says I'm giving planes.
Is it possible to somehow get the point, where they intersect ?
For numericals, one could take a=1 and n=4.
Edit: Being unsure what the correct equation for the line is.
#11 Re: Help Me ! » interatomic forces? » 2022-12-09 15:33:32
#12 This is Cool » Superellipse » 2022-12-08 19:53:45
- mathdrop
- Replies: 0
Superellipse on Wikipedia.
|x/a|^n+|y/b|^n=1 where n>=2
<=>
|y/b|^n=1-|x/a|^n
<=>
y/b=+/- (1-|x/a|^n)^(1/n)
<=>
y=+/- b*(1-|x/a|^n)^(1/n) // absolute makes x<0 usable
a=semi-mayor axis (half-axis in x-direction)
b=semi-minor axis (half-axis in y-direction)
Of course, it has something of the hyperbola.
n=2 leaves the ellipse.
With n increasing from there, the shape converges to a rectangle.
The curvature is 0, where it crosses the axes.
Simplifying it to the supercircle,
which probably is an unsqueezed superelipse, so a=b:

On Wikipedia, they call a supercircle where n=4 a squircle.
Without shifting and variables kept, they give x⁴+y⁴=a⁴ <=> y=+/- (a⁴-x⁴)^(1/4).
With n instead of 4, its the equivalent of a=b in the superelipse-formula at the top.
It seems also to work with a z-part: x^n+y^n+z^n=a^n <=> y=+/- (a^n-x^n-z^n)^(1/n)
Basically I refer to the 2D-Case where z=0, but will expand to 3D at times.
f(x,z,a,n) = (a^n-x^n-z^n)^(1/n)
f'(x,z,a,n) = -x^(n-1)*(a^n-x^n-z^n)^(1/n-1) // slope
f''(x,z,a,n) = -(n-1)*x^(n-2)*(a^n-z^n)*(a^n-x^n-z^n)^(1/n-2) // curvature use for elbowradius
some limit cases:
for n=2 the sqircle is a circle
for n=1 the sqircle is a square
for 0 < n < 1 the sqircle is a star
domain of squircle funtion f(x,z,a,n): // xstart for slope-x-value newton aproxximation (functiondrawing)
a^n-x^n-z^n // content of the root
a^n-z^n-x^n>=0 // which shouldn't be 0 or negative
a^n-z^n>=x^n
x<=(a^n-z^n)^(1/n)
Calculating the area and the perimeter is said to be complicated.
Regarding the area, there is however a shortcut using the Lemniscate Constant L~2.62205755429211981 .
So the area is A=L*sqrt(2)*a^2 . For now I will go with that.
A sidenote before I go deeper into the math:
While browsing the web I stumbled upon a post about a spherefactor-approach.
Below I mainly try to get the n out of the squircle functon.
Instead I throw in more common values out of the hyperbola properties.
c in f(x,a,c) is a counterpart for the semi major axis of a hyperbola
(how far the curve is pulled into an rectangular edge).
r in f(x,a,r) is the radius in the elbow of a hyperbola
(where the highest curvature is).
For the later an n which is described by r and a=r_min,
would probably have to be approximated.
I tried it with the newton procedure, which covered many cases.
The properties I come by may also be interresting for them selves
or handy for other calculations.
For getting the maximum radius (origin to rounded edge)
I'm intersecting the squircle with a line of slope=1:
f(x,a,n)=f(x,z=0,a,n)=(a^n-x^n)^(1/n) // n=4: black line in the graph
g(x)=x // straight 45° ascending line through origin
f(x)=g(x)
solve((a^n - x^n)^(1/n)=x,x)
The computer has not wanted to solve it with n,
but when I tried it with different numbers for n, it took the nth root,
so I've put n there.
x=a/2^(1/n) // simplest positive non-imaginary solution out of 5, n=4: brown line in the graph
y=x since symmetry
a:=r_min // red distance in the graph
d:=r_max // blue distance in the graph
r_max=a/2^(1/n)*sqrt(2)=2^(1/2-1/n)*a
diagonal=r_min*sqrt(2) // blue plus green line in the graph
c:=diagonal-r_max // green line in the graph
c=a*sqrt(2)-a/2^(1/n)*sqrt(2)
=(a-a/2^(1/n))*sqrt(2)=sqrt(2)*(1-2^(-1/n))*a
<=>
a=(2^(1/n-1/2)*c)/(2^(1/n)-1) and 2^(1/n)!=1
<=>
n=-(i*log(2))/(2*π*c_1-i*log((sqrt(2)*a)/(sqrt(2)*a-c)))
and sqrt(2) a!=c and a!=0 and log((sqrt(2)*a)/(sqrt(2)*a-c))+2*i*π*c_1!=0 and c_1 element Z
=log(4)/(2*log(a/(sqrt(2)*a-c))+4*i*π*c_1+log(2)) // variables real
Again without imaginaries:
c=sqrt(2)*(1-2^(-1/n))*a |/sqrt(2)*a
<=>
c/(sqrt(2)*a)=1-2^(-1/n) |-1
<=>
(c/(sqrt(2)*a))-1=-2^(-1/n) |*(-1)
<=>
2^(-1/n)=1-(2^(-1/2)*c/a) |^(-1)
<=>
2^(1/n)=1/(1-(2^(-1/2)*c/a)) |log, 1/(1-(2^(-1/2)*c/a))=(sqrt(2)*a)/(sqrt(2)*a-c)
<=>
1/n=log((sqrt(2)*a)/(sqrt(2)*a-c))/log(2) |^(-1)
<=>
n=log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c))
c'=d/dn=-(a*2^(1/2-1/n)*log(2))/n^2 // for newton approximation
f(x,c,n)=(((2^(1/n-1/2)*c)/(2^(1/n)-1))^n-x^n)^(1/n)
=(2^(1-n/2)*((2^(1/n)-1)/c)^(-n)-x^n)^(1/n) // variables positive
f(x,a,c)=(a^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))-x^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2))))^(log(a/(sqrt(2)*a-c))/log(2)+(2*i*π*c_1)/log(2))*sqrt(a^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))*x^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))*(x^((2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))-a^((2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))))
and -2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)!=0
Without imaginaries:
f(x,a,c)=(a^log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c))-x^log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c)))^(1/log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c)))
=((a^log(2)-x^log(2))/log(c/(sqrt(2)*a-c)+1))^(1/(log(2)*log(c/(sqrt(2)*a-c)+1))) // variables positive
Check:
f(x,c,n)=0 // x-intersect=r_min
(2^(1-n/2)*((2^(1/n)-1)/c)^(-n)-x^n)^(1/n)=0
x=(2^(1-n/2)*((2^(1/n)-1)/c)^(-n))^(1/n)
=(2^(1/n-1/2)*c)/(2^(1/n)-1) and 2^(1/n)!=1 // variables positive
=r_min=a (see above)
Elbow-radius:
r=1/curvature
r=1/f''(a/2^(1/n))
=-(a^(-n)*(a*2^(-1/n))^(2-n)*(a^n-(a*2^(-1/n))^n)^(2-1/n))/(n-1)
=(2^(-1-1/n)*a)/(1-n) // variables positive
For n between ]1,infinity[, this gives half the negative radius.
Why half and why negative ?
Correction by manipulating the numerator (1 -> -2):
r=-2/f''(a/2^(1/n))
=-2*(2^(-1-1/n)*a)/(1-n)
=(2^(-1/n)*a)/(n-1)
<=>
a=2^(1/n)*(n-1)*r and Re(n)<1
<=>
a/r=2^(1/n)*(n-1)
<=>
n=not solvable
r'=d/dn=-(a*2^(-1/n)*(n^2-n*log(2)+log(2)))/((n-1)^2*n^2) // for newton approximation
f(x,r,n)=((2^(1/n)*(n-1)*r)^n-x^n)^(1/n)
=(2*(n-1)^n*r^n-x^n)^(1/n) // variables positive
f(x,a,r)=not findable
f(x,r,n)=0 // x-intersect=r_min
((2^(1/n)*(n-1)*r)^n-x^n)^(1/n)=0
x=((2^(1/n)*(n-1)*r)^n)^(1/n)
=2^(1/n)*n*r-2^(1/n)*r=2^(1/n)*(n-1)*r // variables positive
=r_min=a (see above)
checking it with some limit cases:
for n=2 the sqircle is a circle
r=(2^(-1/n)*a)/(n-1)
r=(2^(-1/2)*a)/(2-1)=a/sqrt(2)
<=>
a=sqrt(2)*r // shouldn't a=r ?
what would that further mean ?:
if r > a/sqrt(2) then its edgy
if r = a/sqrt(2) then its a circle
if r < a/sqrt(2) then its a squirce
for n=1 the sqircle is a square
r=(2^(-1/n)*a)/(n-1)
r=(2^(-1/1)*a)/(1-1)=division by zero, complex infinity
this result seems to be satisfying,
cause a square does have no radius.
for 0 < n < 1 the sqircle is a star
#13 This is Cool » Egg formula » 2022-12-04 21:01:25
- mathdrop
- Replies: 0
The longitudinal cut of an eggshell.
After everything below I hold the opinion, that it is an asymmetric ellipse.
First I digged into Wikipedia.
The cause of the shape of eggs according to an article, linked there, about Mary Caswell Stoddard and her team:
"It begins when an unfertilized egg cell is added to a globule of yolk, and sent down a bird’s oviduct... ...On its travels, it is fertilized by sperm, surrounded by white, and coated in two membranes. The membranes are pumped with fluid like a balloon being inflated, and finally surrounded by a shell. Counter-intuitively, it’s not the shell that matters most, but the membranes. If you dissolve the shell in acid, the naked egg will still retain its original shape."
They took the Baker-Formula and matched bird eggs with it (EggxTractor).
There are different construction methods.
The Wikipedia article also links a paper titled the mathematics of egg shape of Yutaka Nishiyama.
After explaining the Descartes approach, he goes on with the Cassini approach, which is more or less a shortcut of the former.
This could probably be read before taking on the Baker-Formula:
y=t(1+a)^(1/1+a)*(1−a)^(a/1+a)
t=(equatorial diameter)^(-1) ?
a=ln(heightright)/ln(heightleft)
There is another equation which
I struggle to let go of just yet.
It's the Blaschke one, I found on mathtinkering:
x^1.5-l^0.5x+y^2=0
y = ± (sqrt(x)*sqrt(sqrt(a)-sqrt(x)))
Since 2021 this formula of Narushin (see there for variable descriptions) was hyped:
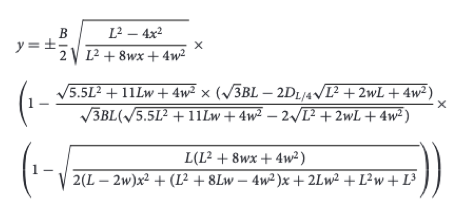
It already has this breadth value,
whch would have been left for me to calculate with the Baker formula
I will see how I like it.
So much for now.
#14 Re: Help Me ! » a ball/torus resting in the tip of a pyramid » 2022-11-23 14:00:38
You're not alone if you do not like linear algebra that much,
but what is geometry without it ?
Maybe I also could have explained it better. It is planeshifting after all.
Is it that I lost you with Hesse Cartesian (or normalized Cartesian equation),
which is the Cartesian version of the Hesse normal form ?
You are almost there, there. Is this one what you call "post 8" ?
There should be English equivalents, but can you follow the mathematical steps of the Germans, there ?:
- Longer German version of the English Hesse normal form Wikipedia site
Point-plane-distance by Hesse Cartesian examples:
- "Daniel Jung" tutoring
- "Simpleclub" aiming at young students
What did you do, when students bailed out on something,
you planed to build on, by the way ? ;-)
#15 Re: Help Me ! » multiplying matrices » 2022-11-23 06:29:07
how would be the procedure again,
if the second matrix would have multiple, lets say 3, columns
and what would that mean ?
#16 Re: Help Me ! » Circle on hyperbola » 2022-11-21 14:09:39
More general approach:
Tangent line: y=m*x+b
Normal line with m=-1/m <= m of tangent line
f(x):=a/b*sqrt(b^2+x^2)
f'(x):=a*x/(b*sqrt(b^2+x^2))
j=:x0
n(x)=-1/f'(t)*(x-t)+f(t) // general normal line equation
n(x,t)=-1/(a*t/(b*sqrt(b^2+t^2)))*(x-t)+a/b*sqrt(b^2+t^2)
= sqrt(b^2+t^2)*(a/b-(b*(x-t))/(a*t))
= (sqrt(b^2+t^2)*(a^2*t+b^2*(t-x)))/(a*b*t)
=-b*x*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a
q=:A1 // q=0 => circlecenter on y-axis
t=:C1
n(0,t)=((a^2+b^2)*sqrt(b^2+t^2))/(a*b)
=(a*sqrt(b^2+t^2))/b+(b*sqrt(b^2+t^2))/a
n(t,t)=a/b*sqrt(b^2+t^2)=f(t)
t²+(n(0,t)-n(t,t))² = r² // pythagoras
<=>
r(t)=sqrt(t²+(n(0,t)-n(t,t))²)
r(t)=sqrt((b^4+a^2*t^2+b^2*t^2)/a^2)
=sqrt((b^4+(a^2+b^2)*t^2)/a^2) // a,b,r real and positive
t(r)=+/- sqrt(-b^4+a^2*r^2)/sqrt(a^2+b^2)
=+/- sqrt((a^2*r^2-b^4)/(a^2+b^2)) // a,b,r real
r(0)=r(t), a=6, b=3, t=4 gives sqrt(89)/2~4,72
n(x,r)=sqrt((a^2*(b^2+r^2))/(a^2+b^2))*((b*(sqrt((a^2*r^2-b^4)/(a^2+b^2))-x))/(a*sqrt((a^2*r^2-b^4)/(a^2+b^2)))+a/b)
n(0,~4.72), a=6,b=3 = n(x,r), a=6, b=3, x=0, r=sqrt(89)/2 = 12.5
Still more general with shifting of the circle:
Tangent line: y=m*x+b
Normal line with m=-1/m <= m of tangent line
f(x):=a/b*sqrt(b^2+x^2)
f'(x):=a*x/(b*sqrt(b^2+x^2))
j=:x0
n(x)=-1/f'(t)*(x-t)+f(t) // general normal line equation
n(x,t)=-1/(a*t/(b*sqrt(b^2+t^2)))*(x-t)+a/b*sqrt(b^2+t^2)
= sqrt(b^2+t^2)*(a/b-(b*(x-t))/(a*t))
= (sqrt(b^2+t^2)*(a^2*t+b^2*(t-x)))/(a*b*t)
=-b*x*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a
q=:A1 // q=0 => circlecenter on y-axis
t=:C1
n(q,t)=-b*q*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a
n(t,t)=a/b*sqrt(b^2+t^2)=f(t)
t²+(n(q,t)-n(t,t))² = r² // pythagoras
<=>
r(q,t)=sqrt(t²+(n(q,t)-n(t,t))²)
r(q,t)=sqrt(t²+(-b*q*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a-a*sqrt(b^2+t^2)/b)²)
=sqrt((a^2*t^4+b^4*(t-q)^2+b^2*t^2*(t-q)^2)/(a^2*t^2))
=sqrt(a^2*t^4+b^4*(t-q)^2+b^2*t^2*(t-q)^2)/(a*t) // a,b,q,t positive
t(r,q) = four long equations. taking the last where everything goes in positive:
t(r,q) = (q*b^2)/(2*(a^2+b^2))+1/2*sqrt((q^2*b^4)/(a^2+b^2)^2-(2*(b^4+q^2*b^2-a^2*r^2))/(3*(a^2+b^2))+(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)/(3*2^(1/3)*(a^2+b^2))+(2^(1/3)*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2))/(3*(a^2+b^2)*(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)))+1/2*sqrt((2*q^2*b^4)/(a^2+b^2)^2-(4*(b^4+q^2*b^2-a^2*r^2))/(3*(a^2+b^2))-(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)/(3*2^(1/3)*(a^2+b^2))-(2^(1/3)*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2))/(3*(a^2+b^2)*(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3))+((8*q^3*b^6)/(a^2+b^2)^3+(16*q*b^4)/(a^2+b^2)-(8*q*(b^4+q^2*b^2-a^2*r^2)*b^2)/(a^2+b^2)^2)/(4*sqrt((q^2*b^4)/(a^2+b^2)^2-(2*(b^4+q^2*b^2-a^2*r^2))/(3*(a^2+b^2))+(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)/(3*2^(1/3)*(a^2+b^2))+(2^(1/3)*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2))/(3*(a^2+b^2)*(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)))))
n(x,t(r,q)) should give the y-value of the circlecenter on x=q
n(x,t(r,q)), a=6, b=3, q=0, r=sqrt(89)/2 and wxMaxima says "division by zero" :-(
What it seems to say is that i should use the approximate procedure, when there is circleshifting
and the exact procedure if the center of the circle lies on the y-axis. So I was not that wrong.
#17 Re: Help Me ! » Circle on hyperbola » 2022-11-21 10:44:18
I'm trying to do the peakvalue-approach with your example here:
Tangent line: y=m*x+b
Normal line with m=-1/m <= m of tangent line
f(x)=2*sqrt(9+x²)
f'(x)=2*x/sqrt(9+x²)
n(x)=-1/f'(t)*(x-t)+f(t) // general normal line equation
n(x,t)=-1/(2*t/sqrt(9+t²))*(x-t)+2*sqrt(9+t²)
=2*sqrt(t^2+9)-(sqrt(t^2+9)*(x-t))/(2*t)
=(5*sqrt(t^2+9))/2 - (sqrt(t^2+9)*x)/(2*t)
=+/- (sqrt(t^2+9)*(5*t-x))/(2*t)
n(x,t):=(sqrt(t^2+9)*(5*t-x))/(2*t)
n(0,t)=(5/2)*sqrt(t^2+9)
n(t,t)=2*sqrt(t^2+9)=f(t)
t²+(n(0,t)-n(t,t))² = r² // pythagoras
r(t)=sqrt(t²+(n(0,t)-n(t,t))²)
r(t)=sqrt(t²+((5/2)*sqrt(t^2+9)-2*sqrt(t^2+9))²)=1/2*sqrt(5*t^2+9)
<=>
t(r)=+/- sqrt(4*r^2-9)/sqrt(5)
r(t): r(4)=1/2*sqrt(5*4^2+9)=sqrt(89)/2=sqrt(22.25)~4.72 gives your radius, see ?
n(x,r)=sqrt(r^2+9)*(sqrt(5)-x/sqrt(4*r^2-9))
=sqrt(5)*sqrt(r^2 + 9)-(sqrt(r^2+9)*x)/sqrt(4*r^2-9)
n(0,r)=sqrt(5)*sqrt(r^2+9)
n(0,~4.72)=sqrt(5)*sqrt((sqrt(89)/2)^2+9)=12.5 your y-circlecenter, see ?
Bob, it seems, that you had the critical hint, this time. Thank you.
Regarding peekvalue, the minimal radius is the one
of a circle with the curvature of the hyperbola in x=0 (see graph).
Edit: saving in between
#18 Re: Help Me ! » Circle on hyperbola » 2022-11-20 16:55:10
f(x)=2*sqrt(9+x²)
f'(x)=2*x/sqrt(9+x²)
x_test_1 ~ sin(63.4)*4.72 = sin(atan(2))*sqrt(22.25) ~ 4.22
(sin(atan(2))*sqrt(22.25))² = 17.8
9+17.8 = 26.8
f'(~4.22) = 2*sin(atan(2))*sqrt(22.25)/sqrt(9+(sin(atan(2))*sqrt(22.25))²)
= 2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)
~ 1.62
atan(~1.62)=atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8))~58.5
x_test_2 ~ sin(58.5)*4.72 = sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)~4.02
(sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25))² = 16 + 81/490
9 + 16 + 81/490 = 25 + 81/490
f'(~4.02) = 2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(9+(sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25))²)
= 2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(25+81/490)
~ 1.60
atan(~1.60)=atan(2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(25+81/490))~58.0
x_test_3 ~ sin(58.0)*4.72 = sin(atan(2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(25+81/490)))*sqrt(22.25)~4.00
I don't mean to brag, but you see how fast it converges ? ;-)
With 3 significant digits it rounds to your exact number solution after only 3 iterations.
And it is applicable to another range of problems,
where exact numbers are perhaps not possible
(but very close ones probably are).
Do you follow my approach ?
The computer gives me wrong values, if I automate it completely.
Then I thought I could ask if I'm doing it right, but obviously it works on paper.
Regarding the word I heath some especially for hyperbolas.
I can put it if I come across it again.
Edit: saving in between
#19 Re: Help Me ! » Circle on hyperbola » 2022-11-06 19:26:02
Thank you for the example with the nice numbers and the hint regarding GeoGebra.
Once, I looked at it shortly, but haven't thought it is that powerful.
Why are you almost the only one who is answering me ?
For my approach I would start out with the angle of the hyperbolas asymptotes alpha.
In English, you probably have a special word for them. Which is it again ?
Applying my approach:
alpha=atan(slope)
alpha=atan(+/- a/b)
alpha=atan(6/3)=atan(2)~63.4
sin(a)=opposite/hypotenuse
sin(a)*hypotenuse=opposite
sin(a)*r=x_offset
sin(atan(2))*sqrt(22.25)=~4.22
x_circle:=0
x_circle+x_offset=x_test_1
I'm going to continue here later.
Edit: alpha in degrees instead of radians, sine instead of cosine
#20 Re: Help Me ! » Circle on hyperbola » 2022-11-06 15:41:18
(a*sqrt(b^2+x^2))/b = a/b*sqrt(b^2+x^2) // haven't initially seen this
Graphing your pickings (and my model of thinking) with GeoGebra:
Old graph, which Bob referred to
Following your proceeding:
f'(x)=2*x/sqrt(9+x²)
f'(4)=2*4/sqrt(9+4²)=8/sqrt(9+16)=8/sqrt(25)=8/5
y=m*x+b <=> y-m*x=b | m=(8/5)^(-1)=-5/8, x=4, y=10
b=10-(-5/8*4)=10-(-20/8)=10-(-2.5)=10+2.5=12.5 // y-intercept
This ignores "while the center of the circle matches, or is close to, a given x"
in my questioning. And the radius is constant, as I mentioned later.
Edit: your radius. vector: r=(0-4,12.5-10)=(-4|2.5) |r|=sqrt((-4)²+2.5²)=sqrt(16+6.25)=sqrt(22.25)=sqrt(89)/2~4.716991, new graph
#21 Re: Help Me ! » Circle on hyperbola » 2022-11-03 10:22:09
It seems, that I just can not let go of your procedure yet.
How have you found what you call nice numbers ?
Another approach for what you gave me:
Where the distance between (a,b) and (c,d)
is the shortest, there is your circle.
Matching your second plot, it must be (6*sqrt(4²+x²))/4 <=> 3/2*sqrt(16+x²),
so a=6 and b=4, there. The x-value of the circles center is 4.
It's radius also is not a whole number. One could round it down to 2,
so I would pick 2. Such is what I thought about.
Can you give a solution to this, too ?
=> I'm not sure if it even is mathematically possible,
to answer such a question without an approximate procedure. <=
Or can you teach me otherwise ?
Altering the radius is the answer to another question,
but can your procedure find point B of your second plot,
if you alter the radius again (as drawn in the plot) ?
Edit: Remarking peak-value-approach for what you gave me.
#22 Re: Help Me ! » Circle on circle » 2022-11-03 08:42:50
With the vertical movement, I mentioned In my last post,
I started to go more general as in the perspective, I started out with,
so horizontal movements should be enough.
I also move the small circle horizontally, and not perhaps along the blue line in your plot
(I missed to mention this while answering to your graph).
To imagine it, you could put the center of the small circle one square above the center of the big circle
and move the small circle horizontally (I imagine to the right) until it touches the big circle.
Known is b, c, d and the two radiuses of the circles.
Unknown is a (I probably should have omitted calling x an unknown in the threadstarter).
Edit: a must also be determined.
#23 Re: Help Me ! » Circle on hyperbola » 2022-11-03 07:43:58
At this point I have been looking for values to start out with.
It could probably help if you would denote your pickings and solutions, here.
Your x-value for the center of the circle is 0. What if it weren't 0 ?
In (a*sqrt(b^2+x^2))/b you have taken a=6 (also y-intercept) and b=3 (sqrt(9)).
Why have you picked such an uneven radius or is it part of a solution ?
According to your description,
there is no radius length in your equations.
Since the radius is constant, this could be a problem.
Following your approach a few steps:
A=(x1,y1); B(x2,y2)
m=((x2-x1)/(y2-y1))
A=(p,q); B(s,t)
m=((s-p)/(t-q))
g(x)=m*x+b
g(x):=((s-p)/(t-q))*x+b
g'(x):=(s-p)/(t-q)=d/dx(g(x)) // 1st derivative
f(x):=2*sqrt(9+x²)
f'(x):=2*x/sqrt(9+x²)=d/dx(f(x)) // 1st derivative
g'(x)*f'(x)=-1 // perpedicularity
(((s-p)/(t-q))*x+b)*(2*x*sqrt(9+x²))=-1
What have you done from there ?
I'm going to outline my approach in a separate posting.
Edit: Correcting mistake in f'(x)
#24 Re: Help Me ! » Circle on hyperbola » 2022-11-02 09:28:13
What does A and B mean in your last post ?
I would need an x-value for the center of the circle.
#25 Re: Help Me ! » Circle on circle » 2022-11-02 08:45:03
Regrading abcd one is unknown and the others are known,
so I move one circle either along x or y.
Can't believe I haven't seen the Pythagoras and maybe the other one.
However, I do not see how I might utilize this here yet,
and I still do not know why you do (1) - (2) + (3).
This is an intersection approach without considering the line
and any slopes:
(x-a)²+(y-b)²=r² <=> (x-a)²+(y-b)²-r²=0
(x-c)²+(y-d)²=s² <=> (x-c)²+(y-d)²-s²=0
Intersecting the circles:
(x-a)²+(y-b)²-r²=(x-c)²+(y-d)²-s² <=> f(x)=y=(a^2-2*a*x+b^2-c^2+2*c*x-d^2-r^2+s^2)/(2*b-2*d)
Somehow there should now be this cases:
0 solutions, 1 solution, 2 solutions.
But it says, that all reals are solutions.
Any clue ?